All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1: 
Question 2: 12 seconds; 
Question 3: 
Question 4: 
Question 5: 
Question 6: 
Question 7: Sample; 
Question 8: 
Question 9: 
Question 10: 
Question 11: 
; do not reject 
(a) 
(b) 
When 
, then 
.
When 
seconds
(c)
When , then .
When 
m.
(a) Using GC, 
.
.
The modulus is 
and the argument is 
(b) Please do label the axes appropriately.
(c)
Let 
, for 
.
Then 
.
Using GC, 
.
Thus, 
and 
.
(a) 
.
(b) 
Note: must write answer in single fraction as requested.
(c) 
Thus, 
.
(d)
We want 
.
Using GC, 
.
(a) 
![V = \pi \big[ r^2 y - \frac{1}{3} y^3 \big]_{r-h}^r](http://theculture.sg/wp-content/ql-cache/quicklatex.com-fa92360544b8f6419933bf0c23a50039_l3.png "Rendered by QuickLaTeX.com")
![V = \pi \big[ r^3 - \frac{1}{3}r^3 - r^2(r - h) + \frac{1}{3} (r - h)^3 \big]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-7325886f375a38d57da1b2c70eaae291_l3.png "Rendered by QuickLaTeX.com")
![V = \pi \big[ \frac{2}{3}r^3 - r^3 + r^2 h + \frac{1}{3} (r^3 - 3r^2 h + 3rh^2 - h^3) \big]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-b935592ed7097d509b904be0d7ad0f98_l3.png "Rendered by QuickLaTeX.com")
![V = \pi \big[ \frac{1}{3} ( 3rh^2 - h^3) \big]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-d3ce45b1429e8b20d9424b19775aa147_l3.png "Rendered by QuickLaTeX.com")
(b) Let 
.
Using GC, 
since 
.
(c) We have to consider a shape smaller. In this case, it will be smaller than hemisphere. We take the volume removed from the bottom and minus the volume found above. Other words, and
Required volume 
(a) Observe that we can simplify it to probability of getting the same as immediately before as 
and probability of getting a different as immediately before as 
.
The probability that A wins is
(b) The probability that B wins in his second round is 
.
The probability that B wins is 
.
The required conditional probability that B wins in his second round given that he won is 
(a) These 53 employees form a sample as they are observations of the population of 75 employees in the Staffing department.
(b) She needs to collect a sample that is random such that each employee has an equal chance of being selected, independently of each other. She can do so by numbering the employees and using a random number generator to select the corresponding employee. By doing so, she can avoid bias and obtain a representative sample.
(c) We have mainly three cases.
Case 1: 5 from administration.
Case 2: 4 from administration.
Case 3: 3 from administration.
Total number of ways 
(a) 
(b) Observe that the mean is given by 
. Thus, 
(c) 
(d)
Since 
(a)
Required probability 
(b) This is conditional probability, we are interested in the probability that they both take exactly same route given that both arrive at B.
The probability that both arrive at B is given by 
.
The probability that they both take exactly same route is given by 
.
Required probability
(c) The probability of arriving at C is given by 
.
Using GC, since 
.
(a) The product moment correlation coefficient of 
suggests there is a moderately strong negative linear correlation between distance and price. From the scatter diagram, we observe that as the distance increases, the price decreases decreasingly which suggests a non-linear relationship between distance and price.
(b) The product moment correlation coefficient will have no change as it has no units and is independent of all scale of measurement.
(c) The car is clearly not a fair and representative observation compared to the other data point since this car has different features from teh other 6 cars. Thus, it is an outlier and should be omitted.
(d) Please do label the axes appropriately.
(e) These distances (residuals) may be positive or negative, which may cancel out when we add them up. By squaring these distance (residuals), we ensure that they are all positive and the sum of this residuals squared will be more meaningful as they will not cancel out. The method of least squares seeks to produce a best-fit line when the sum of these residuals squared are minimised.
(f) Using the GC, the least squares regression line is given by 
(3 s.f.)
Product moment correlation coefficient 
(g) Let 
pounds sterling
The estimate is not reliable as 
lies outside of the data range of ![[2.20, 11.2]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-0c6030566ee4e2bfb46f8ce6b2734602_l3.png "Rendered by QuickLaTeX.com")
and this is extrapolation.
(a)
Let 
be Zhou’s time, in seconds. 
Let 
be Tan’s time, in seconds. 
Then 
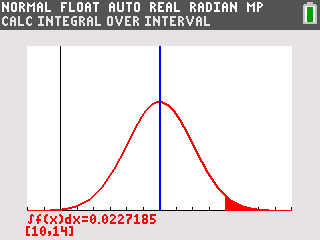
Required probability 
(b)
Unbiased estimate of population mean 
seconds
Unbiased estimate of population variance 
(c)
Let 
be the population mean time Zhou takes to swim 100 metres freestyle, in seconds.
Let be the null hypothesis and 
be the alternative hypothesis.
Test 
against 
at 5% level of significance
Under 
.
Test statistic, 
At 5% level of significance, 
Using GC, 
Thus, we do not reject at 5% level of significance and conclude with insufficient evidence that the mean time taken to swim 100 metres freestyle has improved.
(d) Tan should be using a 2-tailed test as he wants to find out if the mean time has changed, i.e., differs from the 79 seconds.
(e) We assume that while he is away, his time he takes to complete a 100 metres freestyle is still normally distributed, i.e., 
. We also assume that the population variance for Tan’s swim times is known, or has not changed from before.
[…] 2022 A-level H2 Mathematics (9758) Paper 2 […]
Leave a CommentCancel reply
thanks for the solution, do you know if failing to remove anomalous pt in Q10 will cause all subsequent parts to be 0? since the r value, equation, calculated values would be different
Hello, hope it doesn’t affect you. But you probably will lose the 2 marks in (f) and 1 mark in (g). The other 1 mark in (g) should be ok if you did explain that it is out of data range, etc.
Thanks for the reply, just curious wouldn’t that be a triple penalty for the same mistake as I would have been already penalised in (d). Also, for (g) I explain that it is within data range as I did take into the anomalous pt. Would I be penalised again?
But it is all answer mark and no method mark.
Hi! Thanks for ur solution 🙂 Could I check the mark allocation for Q 2,5,11 in terms of method marks?
sorry, i do not recall the specific mark distribution. so it is difficult to comment.
Hi, could I know how many marks is 7(a), 10(a) and 11(c)? Thanks!
sorry 7(b) not 7(a)**
sorry, i do not recall the actual marks distribution of them specifically. 11(c) should be 5.
Hello, for the hypothesis testing question I got the same answer here but a lot of my classmates said that it is a new distribution, so the unbiased estimate and CLT should be used. Is this true?
Also for the last question last part, can I say an assumption is that the sample was chosen randomly?
Generally we do know the population variance and question did specify it’s over a long time. Unbiased estimates can always be found and I guess they are also trying to test if students do read and consider the information given to them in exams. Being able to find the unbiased estimates does not imply population variance changes, the sample could be not representative.
So why did they specifically give 30 samples, which is the minium accepted value for a ‘large sample’? If you say they test on the student’s ability to read the question, then shouldn’t this detail be read too?
And, if you assume the distribution does not change, why the last part of the question ask you about 6 samples and assumptions? If ‘from reading the question’, we can already infer that the distribution after the change in training remains normal, then there is no reason to write that as an assumption, since it is ‘given’ already. However, if you are assuming it, means it is not given. Then your point on concluding that Zhou’s new distribution being ‘given’ as normal is wrong.
If you refer to school notes, then its stated then given population variance, use it. else find the unbiased estimate of population variance. So if we know population variance, then there should not be a need to use the unbiased estimate.
In statistics, when we have a sample, we can definitely find the sample parameters and the unbiased estimates. But we are supposed to discern which parameters are meant to be used.
But that part is about the person having a new training regime so shouldn’t variance change
yes he is using a new regime, but he is testing if the population mean changed. the null hypothesis is testing if the population mean, 80 changed. we did not change this population mean to 79 either, due to finding an unbiased estimate of population mean. so we have to be clear about what are the population parameters, sample parameters and unbiased estimate of population parameters.
8a shouldnt variance be +
Yes my bad. Typo. Sorry bout it
For q11 isn’t it a different training regime. Then shouldn’t the variance be the unbiased estimate
If we follow the hypothesis structure, then even school notes made it quite clear that if population variance is given for the normal distribution, then we should use population variance.
I was wondering if the hypothesis test result should be “do not reject H0” since his timing did not go below 80. Thank you
You should be rejecting since p value is less than level of significance
For q11 the hypo testing question, shouldn’t the new variance be used as its a new training regime
If we follow the hypothesis structure, then even school notes made it quite clear that if population variance is given for the normal distribution, then we should use population variance.
hi, thanks for the solution! Do you know how many marks we would lose if we used gc and p-value for question 11?
I dont think it is a problem so long as you did state the test statistic out. since with the test statistic, one can easily find the p value.
For question 8 (a) shouldnt you always add variance?
Yes my bad. Typo. Sorry about it
this was the worse paper i’ve ever done i’ll say my total % for math will be around 55% 😭😭 is that enough to get a B?
Hi man what do you think the % required for B is this year?? I messed up my papers and got roughly 55% is that enough 😭😭😭