All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1: 
Question 2: 
Question 3: 
Question 4: 
Question 5: 
Question 6: 
Question 7: 
Question 8: 
Question 9: 
Question 10: ![\bar{x} \in [0, 1.45] \cup [1.55, 100]; 0.254, 1.46 \times 10^{-4}; 0.0182](http://theculture.sg/wp-content/ql-cache/quicklatex.com-163572c2cb93c022ff1d941da87b3e9f_l3.png "Rendered by QuickLaTeX.com")
Let 
Using GC, 
(a)
(i) [Maximum marks: 2]
(A) The sequence will increase and approach infinity.
(B) The sequence will be a constant, 5.
(ii) [Maximum marks: 2]
(b)
(i) [Maximum marks: 3]
(ii) [Maximum marks: 1]
(c)
(i) [Maximum marks: 2]
![T_n = n^3 - 11n^2 + 4n - [(n-1)^3 - 11(n-1)^2 + 4(n-1)]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-e06ed8c7e03361a5e0887ea17b41aef3_l3.png "Rendered by QuickLaTeX.com")
(ii) [Maximum marks: 2]
since 
.
(i) [Maximum marks: 5]
At 
.
(ii) [Maximum marks: 4]
Required area 
(iii)
(a) [Maximum marks: 1]
Required area 
(b) [Maximum marks: 2]
(i) [Maximum marks: 2]
By Pythagoras’ Theorem,
(ii) [Maximum marks: 5]
Let the required volume be 
.
Let 
(iii)
(a) [Maximum marks: 3]
Let the required total surface area be 
.
(b) [Maximum marks: 1]
It is a square with sides 
cm.
(i) [Maximum marks: 1]
Possible scores 
.
(ii) [Maximum marks: 7]
Let 
be Tina’s score.
We verify that
(iii) [Maximum marks: 2]
Using GC, 
.
(i) [Maximum marks: 2]
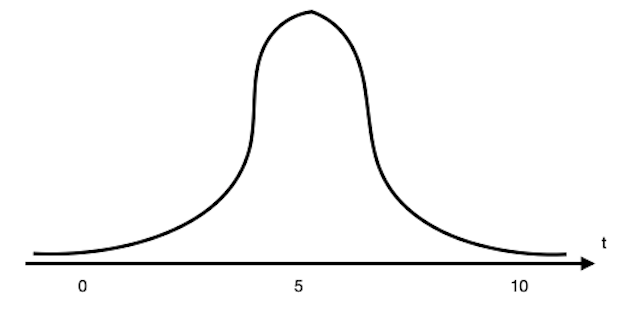
(ii) [Maximum marks: 1]
(iii) [Maximum marks: 2]
(iv) [Maximum marks: 5]
(i) [Maximum marks: 2]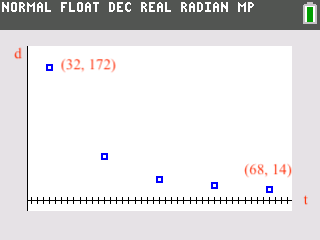
Using GC, 
(ii) [Maximum marks 3]
Using GC, 
(iii) [Maximum marks: 1]
The model does not fit as 
is not within the range of data used by Lim. Thus, extrapolating the data will not be a good and appropriate practice.
(iv) [Maximum marks: 2]
(i) [Maximum marks: 2]
(ii) [Maximum marks: 5]
(i) [Maximum marks: 1]
Each pen in the sample has an equal chance of being selected, independently of each other.
(ii) [Maximum marks: 1]
Let 
be the number of faulty pens, in a sample of 10. 
(iii) [Maximum marks: 4]
Let 
be the number of rejected boxes. 
(iv) [Maximum marks: 5]
Let 
be the number of faulty pens, in a sample of 5. 
Required probability
(v) [Maximum marks: 1]
The alternative testing procedure has a higher chance that a box of 100 pens will be accepted. Thus, less pens are wasted too.
(i) [Maximum marks: 4]
Let 
be the sample mean amount of carbon in each bar.
For 
to be rejected,
![\therefore \bar{x} \in [0, 1.45] \cup [1.55, 100]](http://theculture.sg/wp-content/ql-cache/quicklatex.com-ff42383d0a3a42662dab53e145123a06_l3.png "Rendered by QuickLaTeX.com")
(ii) [Maximum marks: 2]
Since the flat bars are newly launched, the distribution will not be known. By taking a sample of 40, the manager will obtain a sample large enough, the manager can approximate the sample mean weight of the flat bars to a normal distribution by Central Limit Theorem.
(iii) [Maximum marks: 2]
Unbiased estimate of population mean 
Unbiased estimate of population variance ![= \frac{1}{39}[2.586342 - \frac{10.16}{40}] = 1.46 \times 10^{-4}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-c6c591f8534c4b19860e05110c2c441e_l3.png "Rendered by QuickLaTeX.com")
(iv) [Maximum marks: 5]
Let 
be the amount of carbon in the flat bars and 
be the population mean amount of carbon in the flat bars, in percentage.
Under , 
approximately by Central Limit Theorem.
Test statistic, 
, where 
Using a GC to perform a 1-tailed test at 2.5% level of significance, 
.
Since 
, we reject at 2.5% level of significance and conclude with sufficient evidence that the mean amount of carbon is more than 0.25%.
perhaps question 10 upper limit should be 100 since it’s percentage
Thats true. Good point. Thanks.
Any thoughts on this year’s math papers?
when you scale x by factor 2, wouldnt x be (x/2) and hence area should be 1.5 times?
the 2 way stretch results in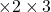
.
Why is there pi in 4(ii)? Isn’t it a square base though.
my bad. doesn’t affect the final answer. thanks
is qn 9iii 0.0535 instead of 0.535?
indeed, copied wrongly off the GC. Thank you.
is qn 9iii 0.0535 instead of 0.535?
indeed, copied wrongly off the GC. Thank you.
9(iii) 0.0535?
indeed, copied wrongly off the GC. Thank you.
should q9 be 0.0535 instead of 0.535?
indeed, copied wrongly off the GC. Thank you.
for q3, isnt the limit for the area under the parametric eqn from t=1/6 to t=2, instead of from t=0.5? when y=0, t=1/6?