2019 A-level H2 Mathematics (9758) Paper 2 Suggested Solutions

All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

Numerical Answers (workings/explanations are after the numerical answers.)

Question 1: $- \frac{2}{3} x (1-x)^{3/2} - \frac{4}{15}(1-x)^{5/2} + C_1;~ - \frac{2}{3} (1-x)^{3/2} + \frac{2}{5}(1-x)^{5/2} + C_2$
Question 2: $x < - \frac{8}{3} \text{~or~} 1 < x < 2;~ - \frac{8}{3} < x < 1 \text{~or~} x >2$
Question 3: $r = \sqrt{\frac{150}{\pi}}, V = \frac{1500 \sqrt{6 \pi}}{\pi};~ r: h = 1:2$
Question 4: $f(x) \approx 1 + 2x^2;~ 0.02001;~0.02001$
Question 5: $\vec{OX} = \textbf{b} + \frac{5}{4} \textbf{a};~ \vec{OY} = \frac{10}{3} \textbf{a} + \frac{8}{3} \textbf{b};~ 3: 8$
Question 6: $7.24 \times 10^{18}$
Question 7: $0.102;~0.991;~ 45p^2 (1-p)^8;~ p = 0.0689$
Question 8: $\frac{23}{56};~\frac{13}{28};~\frac{1}{55};~\frac{21}{110}$ ; orange bird & yellow bird, orange bird & white rider, white horse & white rider, white horse & yellow bird
Question 9: $H_0: \mu = 750, H_1: \mu \neq 750;~ \bar{x} =756, p \approx 0.0897$
Question 10: $\frac{4}{3};~ (50, 18.6);~ y = -0.3x + 33.6;~ r \approx -0.985;~24.6 \text{km/l}$
Question 11: $0.970; ~0.802;~M \approx 381;~0.846$

(i)
$\int x(1 - x)^{1/2}dx$
$= - \frac{2}{3} x(1 - x)^{3/2} + \int \frac{2}{3}(1-x)^{3/2} dx$
$= - \frac{2}{3} x(1 - x)^{3/2} - \frac{4}{15}(1-x)^{5/2} + C_1$

(ii)
$u^2 = 1 - x \implies 2u \frac{du}{dx} = - 1$
$\int x(1 - x)^{1/2}dx$
$= \int (1-u^2)(u)(-2u) du$
$= \int -2u^2 + 2u^4 du$
$= - \frac{2}{3} u^3 + \frac{2}{5}u^5 + C_2$
$= - \frac{2}{3} (1-x)^{3/2} + \frac{2}{5}(1-x)^{5/2} + C_2$

(iii)
$- \frac{2}{3} x(1 - x)^{3/2} - \frac{4}{15}(1-x)^{5/2} + C_1 - [- \frac{2}{3} (1-x)^{3/2} + \frac{2}{5}(1-x)^{5/2} + C_2]$
$= - \frac{2}{3} x(1 - x)^{3/2} - \frac{4}{15}(1-x)^{5/2} + C_1 + \frac{2}{3} (1-x)^{3/2} - \frac{2}{5}(1-x)^{5/2} - C_2$
$= - \frac{2}{3} (1 - x)^{3/2} ( x - 1 )- \frac{2}{3}(1-x)^{5/2} + C_1 - C_2$
$= - \frac{2}{3} (1 - x)^{3/2} [ x - 1 + (1-x)] + C_1 - C_2$
$= C_1 - C_2$ , a constant.

(i)

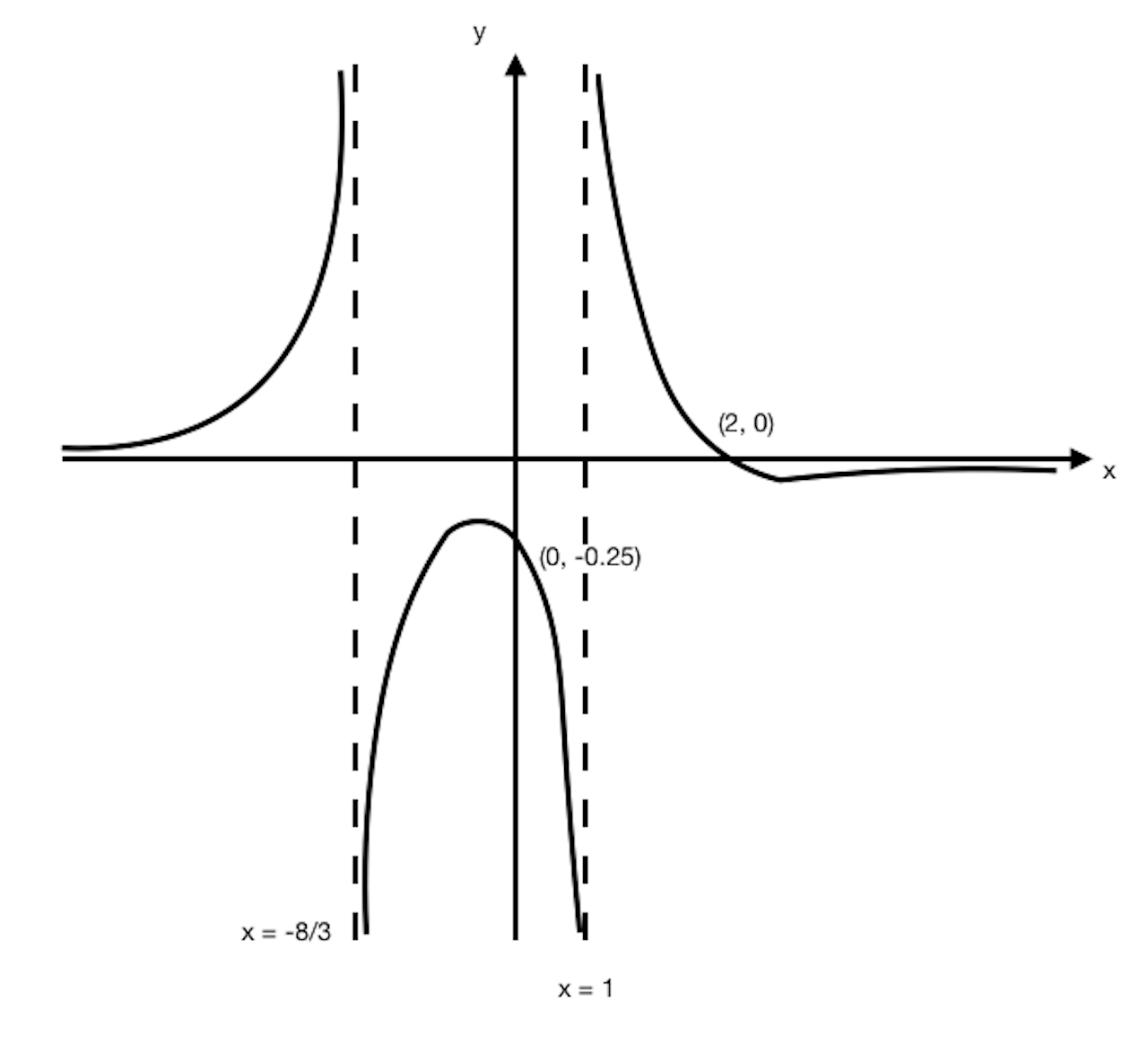
(ii)
From the graph, $x < - \frac{8}{3} \text{~or~} 1 < x < 2$

(iii)
$\frac{x-2}{3x^2+5x-8} >0 \implies \frac{2-x}{3x^2+5x-8} > 0$
$- \frac{8}{3} < x < 1 \text{~or~} x >2$

$2 \pi r^2 + 2\pi r h = 900 \implies h = \frac{900 - 2\pi r^2}{2\pi r}$
$V = \pi r^2 h$
$V = \pi r^2 \bigg(\frac{900 - 2\pi r^2}{2\pi r}\bigg)$
$V = 450r - \pi r^3$
$\frac{dV}{dr} = 450 - 3 \pi r^2$
$\frac{d^2V}{dr^2} = -6 \pi r$
let $\frac{dV}{dr} = 0 \implies r = \sqrt{\frac{150}{\pi}}$
Since $\frac{d^2V}{dr^2} < 0$ , V is maximum when $r = \sqrt{\frac{150}{\pi}}$

$V = 450 \sqrt{\frac{150}{\pi}} - \pi \bigg( \frac{150}{\pi} \bigg)^{3/2}$

$V = \sqrt{\frac{150}{\pi}} \bigg( 450 - \pi \frac{150}{\pi} \bigg)$
$V = \sqrt{300\frac{150}{\pi}}$
$V = \frac{1500 \sqrt{6 \pi}}{\pi}$
$h = \frac{900 - 300}{2 \pi \sqrt{\frac{150}{\pi}}}$
$h = \frac{300}{\sqrt{150\pi}}$
$\frac{r}{h} = \frac{\sqrt{\frac{150}{\pi}}}{\frac{300}{\sqrt{150\pi}}} = \frac{1}{2}$
$\therefore r: h = 1 : 2$

(i)
$f(x) = \sec 2x$
$f'(x) = 2 \sec 2x \tan 2x$
$f''(x) = 4 \sec ^3 2x + 4 \sec 2x \tan^2 2x$
When $x = 0$ ,
$f(0) = 1$
$f'(0) = 0$
$f''(0) = 4$
$f(x) = 1 + 2 x^2 + \ldots$

(ii)
$\int_0^{0.02} \sec 2x dx \approx \int_0^{0.02} 1 + 2x^2 dx \approx 0.02001$

(ii)
$\int_0^{0.02} \sec 2x dx \approx 0.02001$

(iv)
We observe that the answers found in (ii) and (iii) are accurate up to 5 decimal places. As the maclaurin’s series is centred about $x =0$ and the $x$ value used in (ii) and (iii) is close to zero, the approximation is good and accurate.

(v)
We observe that $g(x) = \text{cosec} 2x$ is not defined at $x = 0$ . Thus, the maclaurin’s series cannot be used.

(i)
$l_{BD} : \textbf{r} = \textbf{b} + \lambda (5 \textbf{a}), \lambda \in \mathbb{R}$
$l_{AC} : \textbf{r} = \textbf{a} + \mu ( \textbf{a} + 4 \textbf{b}), \mu \in \mathbb{R}$
At $X$ ,
$\textbf{b} + \lambda (5 \textbf{a}) = \textbf{a} + \mu ( \textbf{a} + 4 \textbf{b})$
$4 \mu = 1 \implies \mu = \frac{1}{4}$
$\vec{OX} = \textbf{b} + \frac{5}{4} \textbf{a}$

(ii)
$l_{CD}: \textbf{r} = 2 \textbf{a} + 4 \textbf{b} + \gamma (\textbf{b} - \textbf{a}), \gamma \in \mathbb{R}$
Since $O, X$ and $Y$ are collinear,
$k \vec{OX} = \vec{OY}$
$k \bigg( \textbf{b} + \frac{5}{4} \textbf{a} \bigg) = 2 \textbf{a} + 4 \textbf{b} + \gamma (\textbf{b} - \textbf{a})$
$k = 4 + \gamma$
$\frac{5}{4} k = 2 - \gamma$
$k = \frac{8}{3}$
$\gamma = - \frac{4}{3}$
$\vec{OY} = \frac{10}{3} \textbf{a} + \frac{8}{3} \textbf{b}$
$\vec{OX} = \frac{3}{8} \vec{OY} \implies OX : OY = 3: 8$

(i)
These 22 clubs form a population, as they are observations drawn from the 22 clubs in Division one.

(ii)
Dilip can collect a random sample by listing the 100 clubs in order and picking a random number from 1 to 4. For example, he picks the the number 4 and will then sample every fourth club in the list. This will ensure that each club has an equal chance of being selected, independently of each other.

(iii)
Required number of ways $= ^{22}C_5 \times ^{24}C_5 \times ^{26}C_5 \times ^{28}C_5 \approx 7.24 \times 10^{18}$ ways.

(i)
The probability that a randomly chosen mug is faulty is constant throughout.
The event that a randomly chosen mug is faulty is independent of another randomly chosen mug being faulty.

(ii)
$F \sim \text{B}(50, 0.08)$
$\text{P}( X \ge 7) = 1 - \text{P}( X \le 6) = 0.1018717831 \approx 0.102$

(iii)
Let $X$ be the number of days where at least 7 faulty mugs are found.
$X \sim \text{B}(5, 0.1018717831)$
$\text{P}(X \le 2) \approx 0.991$

(iv)
Required probability $= p^2 (1-p)^8 \frac{10!}{8!2!} = 45 p^2 (1-p)^8$

(v)
Required probability $= 0.08 \times 0.92 \times 2! \times (1-p)^2 + 0.92^2 \times p(1-p) \times 2 ! + 0.92^2 \times (1-p)^2$
$\implies 0.97 = 0.08 \times 0.92 \times 2! \times (1-p)^2 + 0.92^2 \times p(1-p) \times 2 ! + 0.92^2 \times (1-p)^2$
$0.97 = 0.1472 \times (1-p)^2 + 1.6928 \times p(1-p) + 0.8464 \times (1-p)^2$
$0.97 = 0.9936 \times (1-p)^2 + 1.6928 \times p(1-p)$
$0.97 = (0.9936 +0.6992p)(1-p)$
$p = 0.0689$

(i)
Required probability $= \frac{23}{56}$

(ii)
Required probability $= \frac{13}{28}$

(iiia)
Required probability $= \frac{1}{55}$

(iiib)
Required probability $= \frac{7}{56} \times \frac{32}{55} \times 2! + \frac{10}{56} \times \frac{7}{55} \times 2! = \frac{21}{110}$

(iii)
Let $x$ and $y$ be number of characters that are Gerri’s two favourites.
$\frac{x}{56} \times \frac{y}{55} \times 2 ! = \frac{1}{77}$
$\implies xy = 20$
We need the number of characters to give a product of 20. Thus the possible combinations are:
Orange Bird & Yellow Bird,
Orange Bird & White Rider,
White Horse & White Rider,
White Horse & Yellow Bird

(i)
Manager should carry out a 2-tail test since he wants to find out if the resistance differs from 750 ohms.
Let $\mu$ denote the population mean resistance of the resistor.
Let $H_0$ and $H_1$ denote the null hypothesis and alternative hypothesis respectively.
$H_0: \mu = 750$
$H_1: \mu \neq 750$

(ii)
Sample mean $= 756$
Under $H_0, \bar{X} \sim \text{N} ( 750, \frac{100}{8} )$
Test statistics, $Z = \frac{\bar{X} - 750}{\frac{10}{\sqrt{8}}} \sim \text{N}(0,1)$
Using the GC to perform a 2-tailed test, we have that $p-\text{value} \approx 0.0897$
Since the $p = 0.0897 > 0.05$ , we do not reject $H_0$ at $5 \%$ level of significance and conclude with insufficient evidence that the mean resistance is not 750 ohms.

(iii)
As the distribution is unknown, a sample size of 30 will be required in order to approximate the sample mean distribution to a normal distribution by Central Limit Theorem. The null hypothesis will be $H_0: \mu = 1250$ instead.

Q10

(i)
(a),(b)

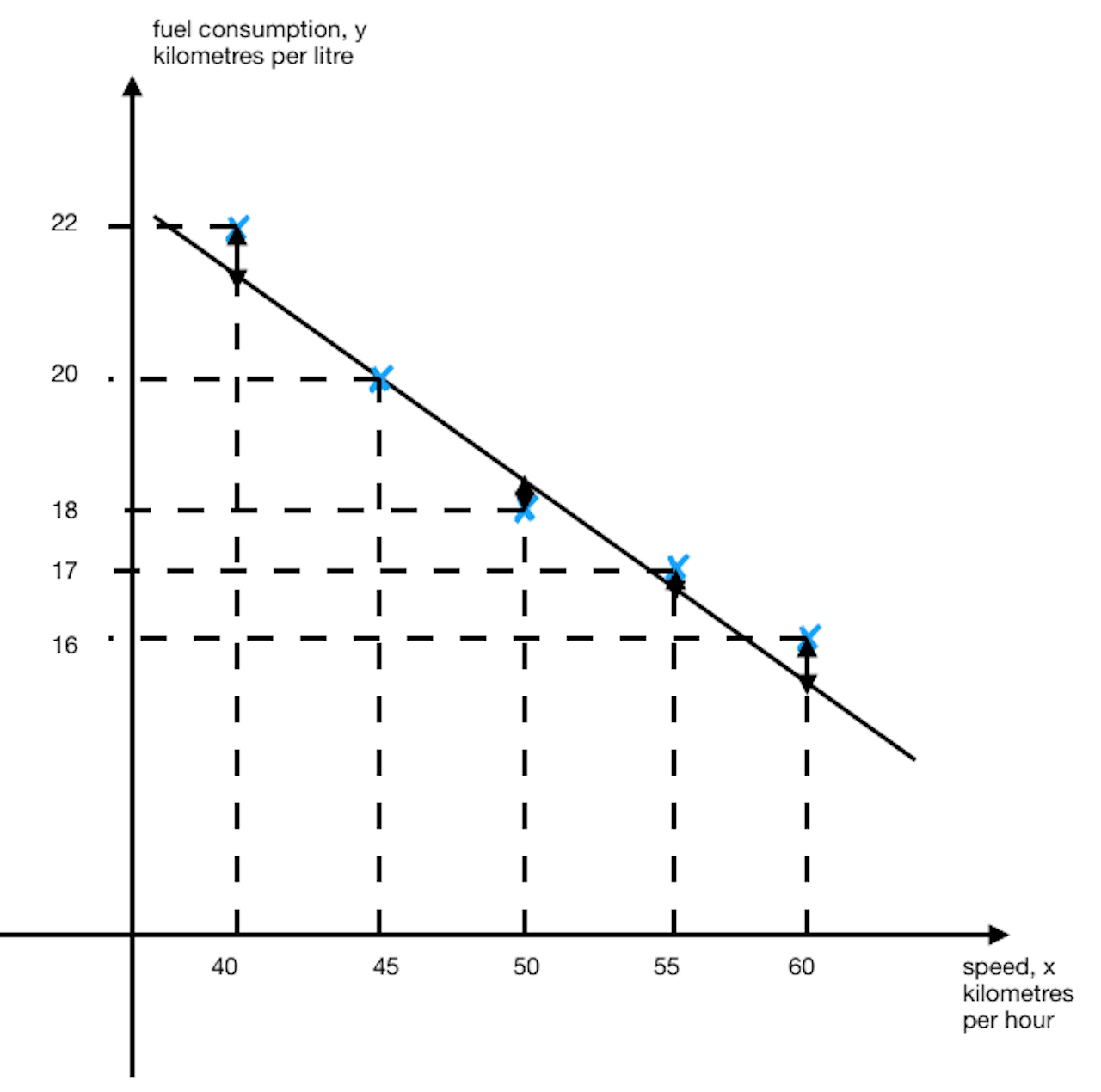
Note that the coordinates (45, 20) should be on the line. Thus no residuals.

(c)
Using GC, sum of the squares of the residuals $= \frac{4}{3}$
(d)
The residuals might result in negative values, thus when finding sum of the residuals, we might have values cancelling each other out. By squaring the residuals, we ensure the values will always be positive.

(ii)
Bhani’s model will give a better fit since it has a smaller value for the sum of the squares of the residuals.

(iii)
The line must pass through the sample mean of the bivariate data, i.e., $(50, 18.6)$

(iv)
$y = -0.3 x + 33.6$
Product moment correlation coefficient $\approx -0.985$

(v)
$y = -0.3(30) + 33.6 = 24.6 \text{km/l}$
The estimate is not reliable as it does not lie within the given data range, thus we are extrapolating.

(vi)
Her data points are a perfectly linear and lies on her line.

Q11

(i)
Let $W$ and $B$ denote the mass of a white and a black ball respectively.
$W \sim \text{N}( 110, 4^2)$
$B \sim \text{N}(55, 2^2)$
$W_1 + \ldots + W_4 \sim \text{N}(440, 64)$
$\text{P}(W_1 + \ldots + W_4 > 425) \approx 0.970$

(ii)
$W + B \sim \text{N}( 165, 20)$
$\text{P}( 161 < W + B < 175 ) \approx 0.802$

(iii)
$W_1 + W_2 + B_1 + B_2 + B_3 \sim \text{N}( 385, 44)$
$\text{P}(W_1 + W_2 + B_1 + B_2 + B_3 < M ) = 0.271$
$\implies M \approx 381$

(iv)
$0.9(B_1 + \ldots + B_4) + 0.7W + R_1 + \ldots + R_4 \sim \text{N}(355, 24.04)$
$\text{P}(0.9(B_1 + \ldots + B_4) + 0.7W + R_1 + \ldots + R_4 > 350) = 0.846$

Relevant materials

MF26

KS Comments

2019 A-level H2 Mathematics (9758) Paper 2 Suggested Solutions2019-09-242021-08-10http://theculture.sg/wp-content/uploads/2018/03/the-culture-logo.pngThe Culture SGhttp://theculture.sg/wp-content/uploads/2017/02/v0zxmzw_-e0-john-mark-kuznietsov.jpg200px200px

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

2019 A-level H2 Mathematics (9758) Paper 2 Suggested Solutions

Relevant materials

KS Comments

Leave a Comment Cancel reply

Leave a Comment
Cancel reply