Solutions to Review 1

Question 1
(i)
$y = f(x) = \frac{x^2 + 14x + 50}{3(x+7)}$

$3y(x+7) = x^2 + 14x + 50$

$x^2 + (14-3y)x + 50 - 21 y = 0$

$\text{discriminant} \ge 0$

$(14-3y)^2 - 4(1)(50-21y) \ge 0$

$196 - 84y + 9y^2 - 200 + 84y \ge 0$

$9y^2 - 4 \ge 0$

$(3y - 2)(3y + 2) \ge 0$

$y \le - \frac{2}{3} \text{~or~} y \ge \frac{2}{3}$

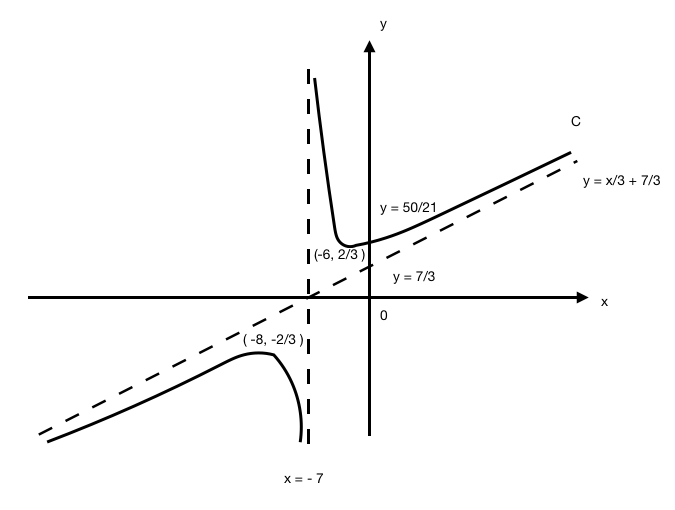
(ii)
Using long division, we find that

$y = \frac{x^2 + 14x + 50}{3(x+7)} = \frac{x}{3} + \frac{7}{3} + \frac{1}{3(x+7)}$

So the asymptotes are $y = \frac{x}{3} + \frac{7}{3}$ and $x = -7$

Curve C of 1(ii)

Question 2
(i)
$x^2 - 9y^2 + 18y = 18$

$x^2 - 9(y^2 - 2y) = 18$

$x^2 - 9[(y-1)^2 - 1^2] = 18$

$x^2 - 9(y-1)^2 + 9 = 18$

$x^2 - 9(y-1)^2 = 9$

$\frac{x^2}{9} - (y-1)^2 = 1$

This is a hyperbola with centre $(0, 1)$ , asymptotes are $y = \pm \frac{x}{3} + 1$ , and vertices $(3, 1)$ and $(-3, 1)$ .

$y = \frac{1}{x^2} + 1$ is a graph with asymptotes $x = 0$ and $y=1$ .

Use GC to plot.

(ii)
$\frac{x^2}{9} - (y-1)^2 = 1$ —(1)

$y = \frac{1}{x^2} + 1$ —(2)

Subst (2) to (1),

$\frac{x^2}{9} - (\frac{1}{x^2} + 1 - 1)^2 = 1$

$\frac{x^2}{9} - (\frac{1}{x^2})^2 = 1$

$x^2 - \frac{9}{x^4} = 9$

$x^6 - 9 = 9x^4$

$x^6 - 9x^4 - 9 = 0$

(iii)
From graph, we observe two intersections. Thus, two roots.

Question 3
(ai)
$\sum_{r=1}^n (r+1)(3r-1)$

$= \sum_{r=1}^n (3r^2 + 2r -1)$

$= \sum_{r=1}^n 3r^2 + \sum_{r=1}^n 2r - \sum_{r=1}^n 1$

$= 3 \sum_{r=1}^n r^2 + 2 \sum_{r=1}^n r - \sum_{r=1}^n 1$

$= 3 \frac{n}{6}(n+1)(2n+1) + 2 \frac{n}{2}(1 + n) - n$

$= \frac{n}{2}(n+1)(2n+1) + n(1+n) - n$

$= \frac{n}{2}(n+1)(2n+1) + n^2$

(aii)
$2 \times 4 + 3 \times 10 + 4 \times 16 + ... + 21 \times 118$

$= 2 [2 \times 2 + 3 \times 5 + 4 \times 8 + ... + 21 \times 59]$

$= 2 [(1+1) \times (3 \cdot 1 - 1) + (2+1) \times (3 \cdot 2 -1) + (3+1) \times (3 \cdot 3 -1) + ... + (20+1) \times (3 \cdot 20 -1) ]$

$= 2 \sum_{r=1}^{20} (r+1)(3r-1)$

$= 2 [\frac{n}{2}(n+1)(2n+1) + n^2 ]$

$= n(n+1)(2n+1) + n^2$

$= n(2n^2 + 3n + 1) + n^2$

$= 2n^3 + 4n^2 + n$

(bi)
$\frac{2}{(r-1)(r+1)} = \frac{A}{r-1} - \frac{B}{r+1}$

$2 = A(r+1) - B(r-1)$

Let $r = -1$

$2 = - B(-2) \Rightarrow B = 1$

Let $r = 1$

$2 = A(2) \Rightarrow A = 1$

$\therefore \frac{2}{(r-1)(r+1)} = \frac{1}{r-1} - \frac{1}{r+1}$

(bii)
$\sum_{r=2}^n \frac{1}{(r-1)(r+1)}$

$= \frac{1}{2} \sum_{r=2}^n \frac{2}{(r-1)(r+1)}$

$= \frac{1}{2} \sum_{r=2}^n (\frac{1}{r-1} - \frac{1}{r+1})$

$= \frac{1}{2} [ 1 - \frac{1}{3}$

$+ \frac{1}{2} - \frac{1}{4}$

$+ \frac{1}{3} - \frac{1}{5}$

$...$

$+ \frac{1}{n-3} - \frac{1}{n-1}$

$+ \frac{1}{n-2} - \frac{1}{n}$

$+ \frac{1}{n-1} - \frac{1}{n+1}]$

$= \frac{1}{2} [1 + \frac{1}{2} - \frac{1}{n} - \frac{1}{n+1}]$

$= \frac{1}{2} (\frac{3}{2} - \frac{n+1+n}{n(n+1)})$

$= \frac{3}{4} - \frac{2n+1}{2n(n+1)}$

(biii)
As $n \to \infty$ , $\frac{1}{n} \to 0$ and $\frac{1}{n+1} \to 0$ , the sum of series tends to $\frac{3}{4}$ , a constant. Thus, series is convergent.

(biv)

$\sum_{r=5}^{n+3} \frac{1}{(r-3)(r-1)}$

Replace $r$ by $r + 2$ . Then we have

$\sum_{r=3}^{n+1} \frac{1}{(r-1)(r+1)}$

$= \sum_{r=2}^{n+1} \frac{1}{(r-1)(r+1)} - \frac{1}{(2-1)(2+1)}$

$= \frac{3}{4} - \frac{2(n+1)+1}{2(n+1)[(n+1)+1]} - \frac{1}{3}$

$= \frac{5}{12} - \frac{2n+3}{2(n+1)(n+2)}$

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Leave a Comment Cancel reply

Leave a Comment
Cancel reply