All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
This is answers for H2 Mathematics (9758). H2 Mathematics (9740), click here.
Numerical Answers (click the questions for workings/explanation)
Question 1: ![]() ;
; ![]()
Question 2: ![]() or
or ![]()
Question 3: ![]() ; Maximum point
; Maximum point
Question 4: ![]() ; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.
; translate the graph 4 units in negative y-direction and translate the graph 2 units in positive x-direction.
Question 5: ![]() ;
; ![]() ;
; ![]() or
or ![]()
Question 6: ![]()
Question 7: ![]() ;
; ![]()
Question 8: ![]() or
or ![]() ;
; ![]() ;
; ![]()
Question 9: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Question 10: ![]() ;
; ![]() ;
; ![]()
Question 11: ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Relevant materials
KS Comments
Firstly, to do well in this paper, student has to be quite intuitive, to be comfortable with the levels of unfamiliarity.
Q1. Simple expansion using MF26. If you used it carefully, it should provide some guidance to Q9(c) actually.
Q2. Simple graphings, using secondary school modulus function knowledge.
Q3. Students have to know how to use ![]() to find back the y-coordinate.
to find back the y-coordinate.
Q4. (a) is even easier if you simply did long division.
Q5. Remainder Theorem from Secondary School for (i). (ii), students need to be alert that when the gradient is ALWAYS positive, the function is strictly increasing, not just increasing.
Q6. Interesting question, that is similar to the Specimen Paper.
Q7. Use of Factor Theorem form MF26 will make this integration much comfortable. By parts work too.
Q8. Standard complex number practice question.
Q9. Very interesting questions. Especially (c), but like mentioned a keen student who did Q1 well, will realise the sum to infinity is simply from MF26.
Q10. Standard vectors questions. Just read carefully and it will be manageable.
Q11. Simple DE too. For the terminal velocity, just need to read that its “after a long time”.
Overall, a manageable paper.
Now things that have yet to come out…
Reciprocal Graph, Area/ Volume, Parametric Equations, Min/Max Problem, APGP, Function, Integration Techniques, Complex Number (Polar Form, Modulus, Argument), Vectors (Planes, Ratio Theorem), Small angle approximation
[…] Paper 1 […]
[…] This is answers for H2 Mathematics (9740). H2 Mathematics (9758), click here. […]
Leave a Comment


![Rendered by QuickLaTeX.com = \Bigg[ \frac{x}{2} - \frac{\text{sin}(4mx)}{2(4m)} + \frac{x}{2} - \frac{\text{sin}(4nx)}{2(4n)} + \frac{1}{4m - 4n}\text{sin} (2mx - 2nx) - \frac{1}{4m + 4n}\text{sin} (2mx + 2nx) \Bigg]_0^{\pi}](https://theculture.sg/wp-content/ql-cache/quicklatex.com-9726903a75641bb76b37d771c061fe4b_l3.png)
![Rendered by QuickLaTeX.com = \Bigg[ \frac{\pi}{2} + 0 + \frac{\pi}{2} - 0 \Bigg]](https://theculture.sg/wp-content/ql-cache/quicklatex.com-ad507faebc29e849ff5755212b06a792_l3.png)
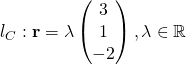
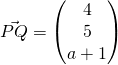
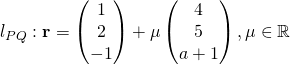
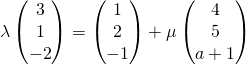 for some
for some 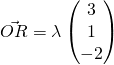 for some
for some 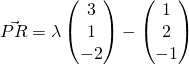
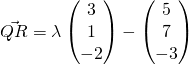
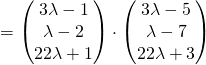


pretty sure 7 part ii is pi,can check for answer using calculator and it gives pi.
yea, my bad. didnt see f(x).. thanks.
Qn 9 part 1 and part 2 check pls?
which parts? cos i’m just rushing it out. thanks
question 10 part ii can use Pythagoras theorem of triangle PRQ and equate the sides together and eventually show lambda has no solution as another way?
definitely. thats similar to showing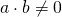 . Effectively proving by contradiction
. Effectively proving by contradiction
hello.. for the last question if i integrate wrongly and did wrongly for the rest of the parts will i get method mark 🙁 i got -k instead of -1/k :((( so i couldnt do the next part also…
will lose method mark for the integration. but your solving, etc is ok then have marks
sigh.. feeling so pessimistic.. qn1 i didnt see the e^2x..
qn6 6 idk what i was doing.. qn 8 i used sum of roots n product if roots but left it there… and my quadratic when i was doing the division i couldnt get 0 as the remainder but i managed to get the answer.. and qn 10 i literally couldn’t do.. 11 careless.. so screwed
how many marks will i get out of 5 if i did the integration wrongly? do i get full credit for next part if my eqn is wrong?
if you final answer to the second part is correct, you can get answer mark. else you will lose the answer mark.
if for part ii for qn 11,i wrote dv/dt=k(10-bv),where k and b are constants and integrated properly like the answer and end up with time 9.21 k seconds(which is wrong as is 9.21),I assume there’s method marks and ecf to a certain extent?
ya will get your method marks one 🙂
Hello. Is this paper the same as H2 9740/01? Cus the answers look more or less similar.
Yes.. only q3, 7, and q11 last part is changed… :/
You can find them here
Is this paper consider as a difficult one? Cus I’m not very confident about the bell curve. Thank you.
q7i i solved using by parts, can you do the working for that question also? thank you!
thats fine too. but i dont really have the time to do it now as I’m trying to do the solutions for the other papers. so sorry bout it. But the answer should be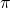 still.
still.
ok thank you!
Hello! can you pls explain qn10? I don’t understand part I. I tried finding |QR| |PR| and |QP| but I didn’t know how to continue… As for part 2, I tried using N as the foot of perpendicular and got RN but i ended up with lumdas and mius, so i couldn’t continue, and ended up dotting with the direction vector of l and labelling it equation 1… As for the shortest distance I took whatever values of RN without substituting any lumdas abd mius in for hopes of a method mark :((( Just want to ask if I’d get any method marks?
I think you might have misinterpreted what the question wanted…

I’ve uploaded the 2017 9740, old syllabus question. Its exactly the same, perhaps it will be clearer for you.
I’m taking the new syllabus, but I don’t really understand the question… So based on what I did I probably won’t get any marks? 🙁
yes. but the old syllabus and the new syllabus have the same question 10.. just the new syllabus had a context. 🙂
Omg for qn 10 iii I thought as small as possible is foot of perpendicular… Sheesh 5 marks gone:((
Do u think for this paper the bell curve would be less steep? I think if I minus that 5 marks I got around 72:(
It can be foot of perpendicular from PR to what you are looking for. Got the same answer doing it via that way
For thr last question last part. I got everything correct so far but copied my equation from my iii answer wrongly…. got the correct shape but i started from 10/k with y=10 as the asymptote. Will i get 0 marks for that?
And for q9, can i leave my answer as 1/4 (n^2)(n+1)^2
10)iii) is it ok if i didnt factorise my surd? Left it as root5/root 2
As for q8)a) i made a careless mistake during expansion and gt a=-b then i used the root formula and gt 1/2 +-… am wondering if i will get working marks for that?
Sighh 9 marks gone due to mistakes like these, dont know if i can still get A for math
Probably can get A la don’t worry
I dont think so? Overall 78% assuming my q6 is entirely wrong cause im not very good in phrasing it in words and as for q9c i got sum to inifity = 0 but the conditions to getting it is really rare so i thought i was wrong and cancelled the entire thing. Kind of sad as getting 90% is easily achievale for the paper so the bellcurve will be really high? Just my 2cents worth
Btw i just realized if the question didnt ask for exact value, you can use your G.C to get the answer and give it in 3sf cuz i went to get the exact answer for every single question lmao
the sum to infinity is just a state question, so it either 1 or nothing. I think in general, most students don’t observe the answer is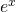 . yes, paper in general is very manageable, compared to 2014 – 2016…
. yes, paper in general is very manageable, compared to 2014 – 2016…
Confirm cant get A. Dont bother.
I’m quite sure you have to rationalize!
I lost 2 marks, can i still get an A?
hi for q10, to prove why it is impossible to be 90, can i complete the square for the quadratic equation, so that is is always positive. As such the dot product will not be 0
thank you
definitely. it gives the same conclusion after all.
hi, q10 iii if i accidentally sub wrong value for c but my method correct will i get method mark for iii and iv?
yup, definitely
Hi for the last question, i did everything correct but last min i changed -kt to -t/k and i switched -1/k with -k during integration (idk why i jst did it). I even got A = 10 and showed k = 0.25, how many marks will i lose?
If for question 5, I leave the answer in exact form instead of decimal, is that fine?
yes, that will be fine too.
for 3ii can i use first derivative to prove?
definitely
Hi for qn 2, i interpreted my own values for the constants a and b, even for labelling the graph, thereafter my workings were all correct. Will i lose too many marks there?
might lose 1 mark. cos not the correct approve. the next part must be in terms of a and b too.
hi for q10ii instead of using discriminant, i solved for lamda and showed that lamda is not a real number if angle PRQ=90. is that acceptable?
for sure. so long as we can prove by contradiction
hi for q10ii, instead of using discriminant to prove, i solved for lamda and showed that lamda is not a real number when angle PRQ=90. is that acceptable?
oops my bad i thought my comment was deleted or something haha
For question 8b,if you use conjugate root thoerm but you expand wrongly and get wrong values, will u get ecf for ii?
will lose the answer marks.
Which is minus 2-3? Or completely 0
Hello!!! Do you think getting an average of 72-75 is very risky for an A??? Cuz I was asking around and some said paper was easy but definitely some ppl also said paper was hard.
I won’t say it’s safe. I hear more easy than hard. And I usually don’t believe students entirely when they say hard.. some are just too harsh on themselves :/
Hi can I just check. For qns 8 part 2. I used the fact that p and q are real so I technically did the conjugate theorm method and solved it so I got the part 3 answer first something like that through comparing coefficients. Is it OK? And I forgot to state since the (coefficients are real) will I lost marks? Pls reply me as I am so worried sick
Sorry, I had some classes yesterday and couldn’t see. It’s okay if you don’t solve the parts in sequence. But the question did say using the values in (bi), so your method should be from there…
For question 8b(i) if you use conjugate root theorem but nerve say explicitly coefficients are real and just used inspection. Will I minus?
Need to explicitly state the real coefficients part, since if it’s not real, then the theorem won’t hold.
But the qns alr say p and q are real so if I never say any thing will I lose the whole 4 marks?
Like basically I did (z-(1-i)) (z-(1+i)) then I say (z^2 -2z +2) then I compare ljke
(Z^2 +aw +29) then I solved for a via inspection and then solve the 2 roots. Including 1+i . So basically I killed one bird with 2 stones but idk if accepted. So I technically got the part c right first. And I never say since coefficients are real I just went straight. Will I lose all 4 marks?
No, won’t lost 4 marks. You still get the method marks for putting p and q in to solve for the two quadratic factors.
As in for the part (2) will I get the marks if I managed to find all the roots? And for p and q
the roots were not required for the question. only p and q. but the part (2) requested students to use the values of p and q to find the factors. not use the roots to find the factors.
Like basically I did (z-(1-i)) (z-(1+i)) then I say (z^2 -2z +2) then I compare ljke
(Z^2 +aw +29) then I solved for a via inspection and then solve the 2 roots. Including 1+i . So basically I killed one bird with 2 stones but idk if accepted. So I technically got the part c right first. And I never say since coefficients are real I just went straight. Will I lose all 4 marks? Because I realised it’s a 4 + 3 marks thing. So will I lose 7? Just because I never state that the coefficients are real
its ok to do by inspection and compare. but it should be the situation when you use p and q as found previously.
I left u a text
For qns 8. Unlike most I basically I did (z-(1-i)) (z-(1+i)) then I say (z^2 -2z +2) then I compare ljke
(Z^2 +aw +29) then I solved for a via inspection which is 4. Then I expand and solve for q and p and then solve the 2 roots. Including 1+i . So basically I killed one bird with 2 stones but idk if accepted. So I technically got the part c right first. And I never say since coefficients are real I just went straight. Will I lose all 7 marks? Pls help as I am worried sick
OH SHIT TEY WERE ASKING FOR W^2
And w^3 fml
Omg if I didn’t find w^2 w^3 and w^4 as I mis read the qns and found all the roots instead and got p and q and could solve for part 3 but without saying as coefficient are real. How many out of the 7 would I lose? I am legit panicking right now and I can’t focus pls help
if you didnt find the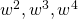 , you lose one mark. for p and q, you dont have to use
, you lose one mark. for p and q, you dont have to use 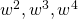 . If its urgent, send me a text at +65 9815 6827. Focus on your other papers.
. If its urgent, send me a text at +65 9815 6827. Focus on your other papers.