Happy 2016 to everyone! I’ve a really exciting news to share now with regards to H2 Mathematics. As I mentioned in a post before, I felt that the current H2 Mathematics can do some upgrading. And yes, the long wait is over, the new syllabus is here. Brace yourself JC1 of 2016 (especially those receiving O’levels soon!). When reading this syllabus, the “integration and applications” is rather important component that should be food for thought. The link to the new Mathematical Formula is also here. Students should always be familiar with what they have in exams, it is, after all their cheat sheet.
H2 Mathematics (2016) This is linked to the syllabus for 2016 A’levels, and don’t worry this syllabus will still be examined in 2017 should students need to retake.
H2 Mathematics (2017) This is what JC1 of 2016 should be looking at. I’ll do a simple comparison later with its predecessor later.
H2 Further Mathematics (2017) This is what most JC1 of 2016 can be looking at. I’m really excited with the launch of this subject and will share a lot on this gradually
Okay so lets start with H2 Mathematics, something that we can compare before looking at H2 Further Mathematics. 🙂 I’ll analyse it based on modules.
H2 Mathematics (9758)
Functions and graphs
We see that the nothing changed for functions, but the new syllabus explicitly mentioned that students do not need to learn how to restrict the domains for composite to exist. Do note that we still must be able to find range of composite functions.
For graphings, the transformation of ![]() is taken out in new syllabus too, while more emphasis is put on conics (finally).
is taken out in new syllabus too, while more emphasis is put on conics (finally).
Inequalities also has more content, focusing on absolute function. To be honest, most of my students are taught this too. Just that the new syllabus state it explicitly.
Sequence and Series
Recurrence seems to be taken out in the new syllabus. So did most students’ favourite Mathematical Induction (Its been brought to Further Mathematics).
Vectors
Nothing much changed in vectors to be honest. Like I told many students, things that can be tested in vectors is as vast as the plane; Examiners can just guide you carefully through the parts to test something.
Complex Numbers
No more De Moivre’s Theorem. Loci is basically taken out. Its rather unfortunate that this is no more.
Calculus
Differentiation has not much changes, though brace yourself for the real world optimisation problems coming your way 🙂
Maclaurin’s is pretty much the same. So is integrations.
But application of integration, we see they state clearly that finding volume with parametric equations won’t be tested (this came out in 2015).
Differential Equations, family of curve is no longer inside. Though questions can still require students to use the curve to analyse. This is also another topics that is very real world.
Statistics
No more Poisson Distribution! But introduction of general discrete random variables. So students now should appreciate it discretely (hopefully)
Which means no more Normal Approximation! And no more free marks for doing continuity correction!
No more T-Test!
No more use of ![]() . I’m pretty some students that took Alevels in 2015 don’t even know this. :/
. I’m pretty some students that took Alevels in 2015 don’t even know this. :/
So yes… It looks as if many topics were skimmed away and modules are made easier. There is always a but…
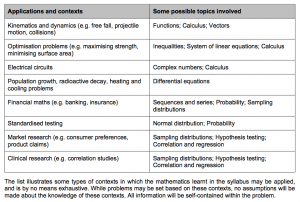
And I think the game changer here integrating the topics and applications. So students should be really careful to check out the scheme of work that has changed as followed.
At the same time, its been explicitly stated in the new syllabus that there will be at least two questions on applications in real-world contexts, from sciences and engineering, in each paper 1 and paper 2. This will truly put students’ understanding to test. They must be able to appreciate and apply effectively. No more doing the ten years series a million times, I’ll say this is similar to the Paper 3 for Science. So it will be important for you to read widely and think out of the box.
H2 Further Mathematics (9649)


[…] time with family, I wrote many sets of applied questions.). You may read more about your syllabus here. Or see the following […]