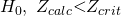2016 A-level H1 Mathematics (8864) Paper 1 Suggested Solutions

All solutions here are SUGGESTED. KS will hold no liability for any errors. Comments are entirely personal opinions.

As these workings and answers are rushed out asap, please pardon me for my mistakes and let me know if there is any typo. Many thanks.
I’ll try my best to attend to the questions as there is H2 Math Paper 2 coming up.

Question 1
(i)
$\frac{d}{dx} [2 \text{ln}(3x^2 +4)]$

$= \frac{12x}{3x^2+4}$

(ii)
$\frac{d}{dx} [\frac{1}{2(1-3x)^2}]$

$= \frac{6}{2(1-3x)^3}$

$= \frac{3}{(1-3x)^3}$

Question 2

$2e^{2x} \ge 9 - 3e^x$

$2u^2 + 3u - 9 \ge 0$

$(2u-3)(u+3) \ge 0$

$\Rightarrow u \le -3 \text{~or~} u \ge \frac{3}{2}$

$e^x \le -3$ (rejected since $e^x > 0$ ) or $e^x \ge \frac{3}{2}$

$\therefore x \ge \text{ln} \frac{3}{2}$

Question 3
(i)

Graph for 3i

(ii)
Using GC, required answer $= -1.606531 \approx -1.61$ (3SF)

(iii)
When $x = 0.5, y = 0.35653066$

$y - 0.35653066 = \frac{-1}{-1.606531}(x-0.5)$

$y = 0.622459 x +0.04530106$

$y = 0.622 x + 0.0453$ (3SF)

(iv)

$\int_0^k e^{-x} -x^2 dx$

$= -e^{-x} - \frac{x^3}{3} \bigl|_0^k$

$= -e^{-k} - \frac{k^3}{3} + 1$

Question 4
(i)
$y = 1 + 6x - 3x^2 -4x^3$

$\frac{dy}{dx} = 6 - 6x - 12x^2$

Let $\frac{dy}{dx} = 0$

$6 - 6x - 12x^2 = 0$

$1 - x - 2x^2 = 0$

$2x^2 + x - 1 = 0$

$x = -1 or \frac{1}{2}$

When $x =-1, y = -4$

When $x = \frac{1}{2}, y = 2.75$

Coordinates $= (-1, -4) \text{~or~} (0.5, 2.75)$

(ii)
$\frac{dy}{dx} = 6 - 6x - 12x^2$

$\frac{d^2y}{dx^2} = - 6 - 24x$

When $x = -1, \frac{d^2y}{dx^2} = 18 > 0$ . So $(-1, -4)$ is a minimum point.

When $x = 0.5, \frac{d^2y}{dx^2} = -18 \textless 0$ . So $(0.5, 2.75)$ is a maximum point.

(iii)

Graph for 4iii

x-intercept $= (-1.59, 0) \text{~and~} (1, 0) \text{~and~} (-0.157, 0)$

(iv)
Using GC, $\int_0.5^1 y dx = 0.9375$

Question 5
(i)
Area of ABEDFCA $= \frac{1}{2}(2x)(2x)\text{sin}60^{\circ} - \frac{1}{2}(y)(y)\text{sin}60^{\circ}$

$2\sqrt{3} = \sqrt{3}x^2 - \frac{\sqrt{3}}{4}y^2$

$2 = x^2 - \frac{y^2}{4}$

$4x^2 - y^2 =8$

(ii)

Perimeter $= 10$

$4x+2y + (2x-y) = 10$

$6x + y = 10$

$y = 10 - 6x$

$4x^2 - (10-6x)^2 = 8$

$4x^2 - 100 +120x -36x^2 = 8$

$32x^2 -120x+108=0$

$x=2.25 \text{~or~} 1.5$

When $x=2.25, y = -3.5$ (rejected since $y >0$ )

When $x=1.5, y = 1$

Question 6
(i)
The store manager has to survey $\frac{1260}{2400} \times 80 = 42$ male students and $\frac{1140}{2400} \times 80 = 38$ female students in the college. He will do random sampling to obtain the required sample.

(ii)
Stratified sampling will give a more representative results of the students expenditure on music annually, compared to simple random sampling.

(iii)
Unbiased estimate of population mean, $\bar{x} = \frac{\sum x}{n} = \frac{312}{80} = 3.9$

Unbiased estimate of population variance, $s^2 = \frac{1}{79}[1328 - \frac{312^2}{80}] = 1.40759 \approx 1.41$

Question 7
(i)
[Venn diagram to be inserted]

(ii)
(a)
$\text{P}(A \cup B) = \text{P}(A) + \text{P}(B) - \text{P}(A \cap B) = 0.8$
(b)
$\text{P}(A \cup B) - \text{P}(A \cap B) = 0.75$

(iii)
$\text{P}(A | B')$

$= \frac{\text{P}(A \cap B')}{\text{P}(B')}$

$= \frac{\text{P}(A) - \text{P}(A \cap B)}{1 - \text{P}(B)}$

$= \frac{0.6 - 0.05}{1-0.25}$

$= \frac{11}{15}$

Question 8
(i)
Required Probability $= \frac{1}{2} \times \frac{3}{10} \times \frac{2}{9} = \frac{1}{30}$

(ii)
Find the probability that we get same color. then consider the complement.

Required Probability $= 1 - \frac{1}{30} - \frac{1}{2} \times \frac{5}{10} \times \frac{4}{9} - \frac{1}{2} \times \frac{2}{10} \times \frac{1}{9} - \frac{1}{2} \times \frac{4}{6} \times \frac{3}{5} - \frac{1}{2} \times \frac{2}{6} \times \frac{1}{5} = \frac{11}{18}$

(iii)
$\text{P}(\text{Both~balls~are~red} | \text{same~color})$

$= \frac{\text{P}(\text{Both~balls~are~red~and~same~color})}{\text{P}(\text{same~color})}$

$= \frac{\text{P}(\text{Both~balls~are~red})}{\text{P}(\text{same~color})}$

$= \frac{1/30}{7/18}$

$= \frac{3}{35}$

Question 9
(i)
Let X denote the number of batteries in a pack of 8 that has a life time of less than two years.

$X \sim B(8, 0.6)$
(a)
Required Probability $=\text{P}(X=8) = 0.01679616 \approx 0.0168$

(b)
Required Probability $=\text{P}(X \ge 4) = 1 - \text{P}(X \le 3) = 0.8263296 \approx 0.826$

(ii)
Let Y denote the number of packs of batteries, out of 4 packs, that has at least half of the batteries having a lifetime of less than two years.

$Y \sim B(4, 0.8263296)$

Required Probability $=\text{P}(Y \le 2) = 0.1417924285 \approx 0.142$

(iii)
Let W denote the number of batteries out of 80 that has a life time of less than two years.

$W \sim B(80, 0.6)$

Since n is large, $np = 48 > 5, n(1-p)=32 >5$

$W \sim N(48, 19.2)$ approximately

Required Probability

$= \text{P}(w \ge 40)$

$= \text{P}(w > 39.5)$ by continuity correction

$= 0.9738011524$
$\approx 0.974$

Question 10
(i)
Let X be the top of speed of cheetahs.
Let $\mu$ be the population mean top speed of cheetahs.

$H_0: \mu = 95$

$H_1: \mu \neq 95$

Under $H_0, \bar{X} \sim N(95, \frac{4.1^2}{40})$

Test Statistic, $Z = \frac{\bar{X}-\mu}{\frac{4.1}{\sqrt{40}}} \sim N(0,1)$

Using GC, $p=0.0449258443 \textless 0.05 \Rightarrow H_0$ is rejected.

…

(ii)
$H_0: \mu = 95$

$H_1: \mu > 95$

For $H_0$ to be not rejected,

$\frac{\bar{x}-95}{\frac{4.1}{\sqrt{40}}} \textless 1.644853626$

$\bar{x} \textless 96.06 \approx 96.0$ (round down to satisfy the inequality)

$\therefore \{ \bar{x} \in \mathbb{R}^+: \bar{x} \textless 96.0 \}$

Question 11
(i)
[Sketch to be inserted]

(ii)
Using GC, $r = 0.9030227 \approx 0.903$ (3SF)

(iii)
Using GC, $y = 0.2936681223 x - 1.88739083$

$y = 0.294 x - 1.89$ (3SF)

(iv)
When $x = 16.9, y = 3.0756 \approx 3.08$ (3SF)

Time taken $= 3.08$ minutes

Estimate is reliable since $x = 16.9$ is within the given data range and $|r|=0.903$ is close to 1.

(v)
Using GC, $r = 0.5682278 \approx 0.568$ (3SF)

(vi)
The answers in (ii) is more likely to represent since $|r|=0.903$ is close to 1. This shows a strong positive linear correlation between x and y.

Question 12
Let X, Y denotes the mass of the individual biscuits and its empty boxes respectively.

$X \sim N(20, 1.1^2)$

$Y \sim N(5, 0.8^2)$

(i)
$\text{P}(X \textless 19) = 0.181651 \approx 0.182$

(ii)
$X_1 + ... + X_12 + Y \sim N(245, 15.16)$

$\text{P}(X_1 + ... + X_12 + Y > 248) = 0.2205021 \approx 0.221$

(iii)
$0.6X \sim N(12, 0.66^2)$

$0.2Y \sim N(1, 0.16^2)$

Let $A=0.6X$ and $B = 0.2Y$

$A_1+...+A_12+B \sim N(145, 5.2528)$

$\text{P}(142 \textless A_1+...+A_12+B \textless 149) = 0.864257 \approx 0.864$

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Showing 51 comments

Elston November 10, 2016
Reply
Hello! I’m not sure whether it’s something wrong with my phone or some other problem like that but I can’t see any of the answers!
- KS Teng November 10, 2016
  Reply
  hi, sorry. but h1 has to wait. H2 was more fun. So I did H2 first..
  - Elston November 10, 2016
    Reply
    Understood! Thanks for your effort!!
Helloooo November 10, 2016
Reply
Hello roughly how much do you need to get in order to get an A in h1 math?
asdfghjkl November 10, 2016
Reply
what time will the answers be out? ESTIMATE PLS
Hello November 10, 2016
Reply
Hi what time will you be uploading the answers?
lydia November 10, 2016
Reply
thanks a lot for trying to upload the ans ASAP!
jam November 10, 2016
Reply
hello! for 6iii), the question mentioned in hundreds of dollars, is there a need to take all the answers x100?
- KS Teng November 10, 2016
  Reply
  no need. since its already defined to be X
  - Elston November 10, 2016
    Reply
    This is an odd question but if you leave the answer as mean=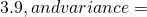 $3.9, and variance=$ 1.41, will I not get the answer mark because of the units? Or is it alright?
    - KS Teng November 10, 2016
      Reply
      the mean is fine. but variance will need to be $$^2$ which is rather awkward.
      - Elston November 10, 2016
        
        I see. Thanks! So I guess that’s one answer mark gone, sighs. Thanks agn!
Nadya November 10, 2016
Reply
Hello! Will the rest of the answers be uploaded as well? Thanks very much for getting all these answers out for us 🙂
- KS Teng November 10, 2016
  Reply
  yea. haha cos I’m having lessons now. But will be out.
millie November 10, 2016
Reply
hi! based on the difficulty of this paper, what mark range do you think A and B will be? 🙂
asdfghjkl November 10, 2016
Reply
hey how can 8ii be a negative probability
- KS Teng November 10, 2016
  Reply
  its a typo. you can just key the answer in yourself.
Jack November 10, 2016
Reply
The probability question is wrg? How can u have a negative probability
- KS Teng November 10, 2016
  Reply
  just key it into the GC yourself. I’m having lessons now for H2 math.
Juju November 10, 2016
Reply
what’s the rough marks to get an A for h1 maths in A levels?
crazekid November 10, 2016
Reply
Hi, I think there is an error in 8(iii), how can it be that your answer in 8(ii) is 11/18 (different balls) and yet you use 11/18 for same balls? I think it should be 1/30 divided by 7/18, giving you an answer of 3/35. Thanks for uploading the answers, greatly appreciate it 🙂
- KS Teng November 10, 2016
  Reply
  hi, thanks for that. cos i’m just blindly typing them on the phone as I’m having H2 Math class now. Too careless.
eeeeee November 10, 2016
Reply
Hello! For Q4iii, isn’t there 3 x intersections?
- KS Teng November 10, 2016
  Reply
  yea, my bad. didnt read the question. sorry, i’ll typing the h1 on the phone while having h2 math classes now. cos i only planned on doing h1 at 10pm lol
  Thanks for pointing it out!
Soon November 10, 2016
Reply
Q4 asking for coordinates that cut x-axis and it should be 3 points (1,0), (-0.157,0), (-1.593,0). Cutting at y-axis is not required
- KS Teng November 10, 2016
  Reply
  oh right. didnt read the question. sorry, i’ll typing the h1 on the phone while having h2 math classes now. cos i only planned on doing h1 at 10pm lol.
  Thanks for pointing it out!
test November 10, 2016
Reply
getting 95/100 will definitely be A even if the bell curve is high right?
- KS Teng November 10, 2016
  Reply
  haha idk. it seems like everybody is getting >90 for this paper… tough moderation.:/
random passerby November 10, 2016
Reply
Just a minor mistake for 11(v) when you rounded it off to 3 s.f the decimal point went missing. Omg I just realised my careless mistakes and how I didn’t x 1/2 for the probability qn I am feeling q depressed now LOL ohwell thanks for uploading the answers for all of us! 🙂 gladly appreciate it 🙂
- KS Teng November 10, 2016
  Reply
  Oops! Thanks so much for pointing that out! Its over! Focus on the papers to come 🙂
Soon November 10, 2016
Reply
why 8(i) need to multiply by 1/2
- random passerby November 10, 2016
  Reply
  You have to pick the box first that’s why x 1/2 I guess! I didn’t do that too bc I was afraid it’ll lead to “double counting” 🙁
  - KS Teng November 10, 2016
    Reply
    Yup, passerby is right. you need to consider which box you’re picking cos they said a box is picked at random. 🙂
Juju November 10, 2016
Reply
For 10ii why do we test the claim at less than 95 instead of more than 95?
J November 10, 2016
Reply
Does anybody know how h1 bellcurves are usually like? Is 70 an A, or really harsh like >90?
- KS Teng November 11, 2016
  Reply
  its harsh. especially given this paper, tough moderation
Soon November 10, 2016
Reply
It is a question that confused us with words. The last part stated ” he finds that the mean top speed….is NOT greater than 95″, which have to reject the Ho that is greater than 95.
- Juju November 10, 2016
  Reply
  oh I see thank you! 🙂
Daphne November 11, 2016
Reply
Hello, I think for Q10ii, you should test for u>95 since Probability of X being more than 95 is not achieved (insufficient evidence to prove H1 is true) and hence H0 is not rejected, and is more than 0.05 (critical region)
P(X > x) > 0.05, hence find X values to satisfy this using sample mean distribution.
No? 🙂
- Daphne November 11, 2016
  Reply
  I took “he finds that mean top speed is not greater than 95…” to refer to the rejection of H1 and to work from this rejection
  - Daphne November 11, 2016
    Reply
    *sry last comment*
    You rejected H0: u = 95 to derive the range of sample mean values.
    But question only stated not more than 95, so there is a possibility of u=95 and u95 and thus not reject H0: u=95 to derive our sample values from there 🙂
    - Daphne November 11, 2016
      Reply
      *Possibility of u=95 and u<95 (less than 95) oh god sorry for the spam just very worried
      - KS Teng November 11, 2016
        
        Hi, yup you’re right. I didnt read carefully enough. thanks! and sorry for the confusion
Lmao November 11, 2016
Reply
For 10 ii, can my alternate hypothesis more than 95? After which I show that Ho is valid, hence mean is not greater than 95.
And questiom 11vi, isnt the p value in part v more accurate? Because the increase in sample size will provide a more accurate representation of the entire population?
- KS Teng November 11, 2016
  Reply
  you’re correct. sorry I forgot to switch the inequality in 10ii
Soon November 11, 2016
Reply
Daphe, thanks for your sharing. Then my mark gone-lah ;-(
- KS Teng November 11, 2016
  Reply
  yea, this question is really tricky. Must really read precisely. :/
Hellohello November 12, 2016
Reply
For 10ii shouldn’t Zcal>Zcritical since we do not reject Ho? Then shouldn’t the answer be 93.sth if I’m not wrong?
- KS Teng November 12, 2016
  Reply
  Hi, this is a right tailed test. So to not reject $H_0, ~ Z_{calc} \textless Z_{crit}$