Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS

So let us now continue study SRS. Recall in part 3, we introduced the idea of unit inclusion probability.
$\pi_i = P(\mathrm{unit~i~in~sample}) = \frac{n}{N}$
Subsequently, we introduced $w_i$ , which is the sampling weight.
$w_i = \frac{1}{\pi_i} = \frac{N}{n}$
The sampling weight of unit i can be interpreted as the number of population units represented by unit i. It is the reciprocal of the inclusion probability after all. And in SRS, each unit has inclusion probability, consequently, all sampling weights are the same. Intuitively, every unit the sample represent itself plus $(\frac{N}{n}-1)$ of the units in the population that were NOT sampled. Thus for an SRS, $\sum_{i \in D} w_i = \sum_{i \in D} \frac{N}{n} = N$ .
Since all weight are the same in an SRS, we can also consider our sample as a self-weighting sample, where every unit has the same sampling weight.

Next, we look at confidence intervals. For those with only A’levels H2 Mathematics knowledge, this is just the reverse of level of significance. Now in statistical analysis, we often start with point estimates (thats what we found previously) and then we measure the accuracy of the estimates, with MSE as introduced. But confidence intervals (CI) is a much convenient approach. An intuitive idea is that we first establish a $\beta\%$ confidence interval. If we take samples from our population over and over again, and construct a confidence interval using our procedure for each possible sample, we expect $\beta \%$ of the resulting intervals to include the true value of the population parameter.

In probability sampling from a finite population, only a finite number of possible samples exist (Recall $N \!C_n$ ) and we know the probability with which each will be chosen. So if we were able to generate all possible samples from the population, we would be able to calculate the exact confidence level required.

In practice, we may not know the values of all possible samples. We consider normal approximation, if n, N, and N – n are sufficiently large ( $\ge 50$ ), then $\frac{\bar{y}- \bar{y_u}}{\sqrt{Var(\bar{y})}} \sim N(0,1)$

Recall that $Var(\bar{y}) = \frac{S^2}{n}(1 - \frac{n}{N})$ , since in reality, we often don’t have $S^2$ , we replace $Var(\bar{y})$ by $\hat{Var}(\bar{y}) = \frac{s^2}{n}(1 - \frac{n}{N})$

Thus, an approximate $100(1 - \alpha) \%$ CI for the population mean is
$(\bar{y} - z_{\alpha / 2} \sqrt{\hat{Var}(\bar{y})}$ , $\bar{y} - z_{\alpha / 2} \sqrt{\hat{Var}(\bar{y})})$
or
$(\bar{y} - z_{\alpha / 2} \sqrt{1 - \frac{n}{N}} \frac{s}{\sqrt{n}}$ , $\bar{y} + z_{\alpha / 2} \sqrt{1 - \frac{n}{N}} \frac{s}{\sqrt{n}})$ .
where $z_{\alpha / 2}$ is the $(1 - \alpha / 2 )^{th}$ percentile of the standard normal distribution.

Now we consider approximate CI for proportion and the rules of thumb is that BOTH $np \ge 5 ~\&~ n(1-p) \ge 5$ , so
$(\hat{p} - z_{\alpha / 2} \sqrt{(1 - \frac{n}{N}) \frac{\hat{p} (1 - \hat{p})}{n-1}}$ , $\hat{p} - z_{\alpha / 2} \sqrt{(1 - \frac{n}{N}) \frac{\hat{p} (1 - \hat{p})}{n-1}})$

The last thing for today is to find out how to estimate the sample size, and of course, what is a “correct” or proper sample size. We remind ourselves that we must balance between the precision of the estimates and the cost of the survey. From part 4, we recall that it is the absolute size of the sample that matters, not the proportion of the population, and the FPC has little effect on the variance of estimates in large populations. The following describes the steps to estimate the sample size:

Specify the tolerable error (confidence level 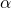$\alpha$ and margin of error $e$ ).
Find an equation relating sample size n and the margin of error.
Estimate any unknown quantities and solve for n.
Evaluate and adjust by repeating the above. This is to ensure you don’t find a sample size that is much larger than you can afford, and adjust some of our expectations.

The tolerable error can be studied from two different perspective, based on what we want to tweak.

Absolute Precision
$P(|\bar{y} - \bar{y_u}| \le e) = 1 - \alpha$
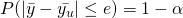
Here, confidence level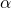 $\alpha$ is usually set at 0.05 and e is simple half-width of the confidence interval.
$e = z_{\alpha / 2} \sqrt{(1 - \frac{n}{N}) \frac{S^2}{n}}$
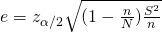
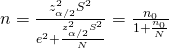$n = \frac{z^2_{\alpha / 2} S^2}{e^2 + \frac{z^2_{\alpha / 2} S^2}{N}} = \frac{n_0}{1 + \frac{n_0}{N}}$ , where 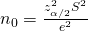$n_0 = \frac{z^2_{\alpha / 2} S^2}{e^2}$ is the sample size for SRS with replacement.
Relative Precision
$P(|\frac{\bar{y} - \bar{y_u}}{\bar{y_u}}| \le e) = 1 - \alpha$
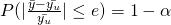
Instead of adjusting the absolute error, we can also control the CV to achieve a desired relative precision. The idea here is to substitute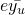 $e \bar{y_u}$ with e.
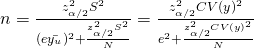$n = \frac{z^2_{\alpha / 2} S^2}{(e \bar{y_u})^2 + \frac{z^2_{\alpha / 2} S^2}{N}} = \frac{z^2_{\alpha / 2} CV (y)^2}{e^2 + \frac{z^2_{\alpha / 2} CV (y)^2}{N}}$ , which is solely determined by CV.

So we should realise by now that CV or $S^2$ must be estimated. Occasionally, we are limited by our data and can’t estimate S. So we make an intelligent guess.

If you believe the population is normally distributed, then S can be roughly estimated by some range/4 or some other range/6. This is because approximately, 95% of values form a normal population are within 2 standard deviations of the mean, and 99.7% of the values are within 3 standard deviations of the mean.
For large population, 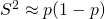$S^2 \approx p(1-p)$ . and clearly the maximum value of 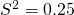$S^2 = 0.25$ . And we can use this value if we have no information on p.

Most surveys in which a proportion is measure, $e = 0.03$ and $\alpha = 0.05$ . And for large population, an even rough estimate at 95% CI, is $e \approx \frac{1}{\sqrt{n}}$ or $n \approx \frac{1}{e^2}$

In general, the larger the sample, the smaller the sampling error.

Sampling & Survey #1 – Introduction
Sampling & Survey #2 – Simple Probability Samples
Sampling & Survey #3 – Simple Random Sampling
Sampling & Survey #4 – Qualities of estimator in SRS
Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS
Sampling & Survey #6 – Systematic Sampling
Sampling & Survey #7 – Stratified Sampling
Sampling & Survey # 8 – Ratio Estimation
Sampling & Survey # 9 – Regression Estimation
Sampling & Survey #10 – Cluster Sampling
Sampling & Survey #11 – Two – Stage Cluster Sampling
Sampling & Survey #12 – Sampling with unequal probabilities (Part 1)
Sampling & Survey #13 – Sampling with unequal probabilities (Part 2)
Sampling & Survey #14 – Nonresponse

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Comments

pingbacks / trackbacks

Sampling & Survey # 9 – Regression Estimation – The Culture
[…] #3 – Simple Random Sampling Sampling & Survey #4 – Qualities of estimator in SRS Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS Sampling & Survey #6 – Systematic Sampling Sampling & Survey #7 – Stratified […]
February 3rd, 2016 09:52 PM

Cart

Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS

Leave a Comment
Cancel reply

Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS

Leave a Comment Cancel reply

Leave a Comment
Cancel reply