The Modulus Sign #4

By KS Teng

I received this from a student of mine who was really confused with the transition from line 2 to line 3. Students should give it a thought before reading my explanation below.

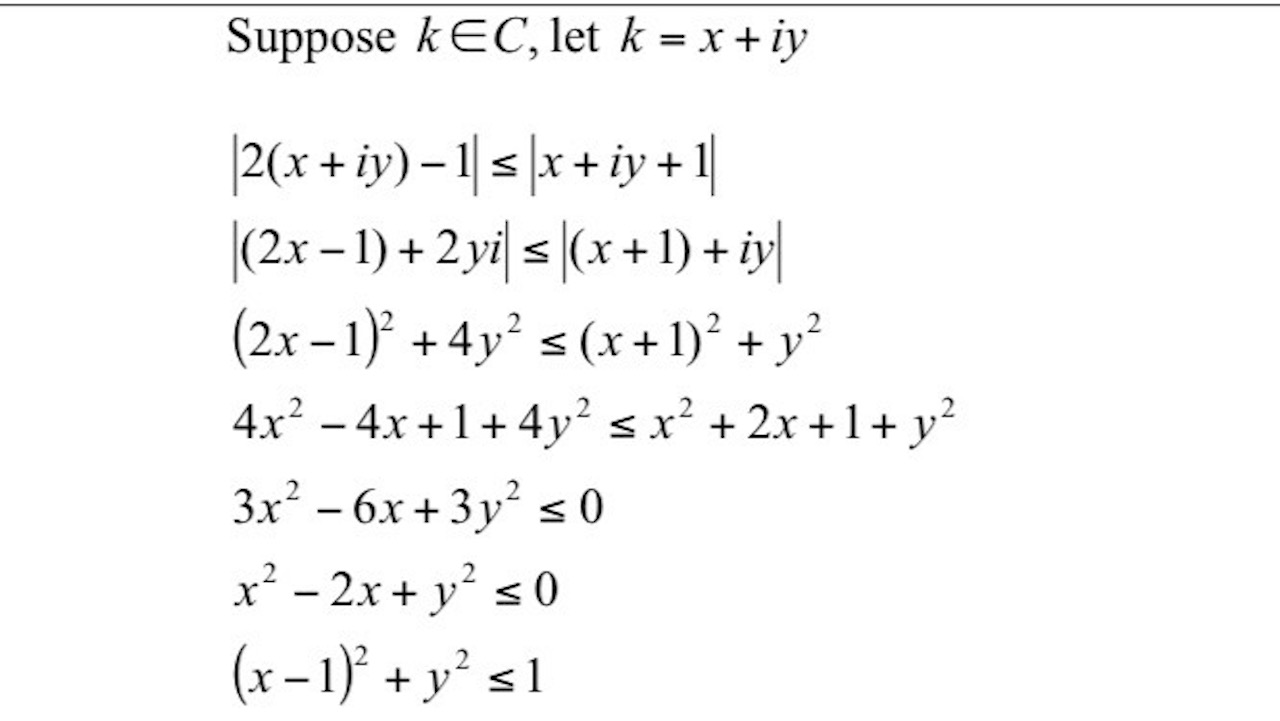
Modulus of a Complex Number

Modulus of a Complex Number

Firstly, my student felt that |(2x-1)+2yi| \le |(x+1)+yi| was being squared on both sides to remove the modulus and the next step should be [(2x-1)+2yi]^{2} \le [(x+1)+yi]^{2}. She is very mistaken, as (2x-1)+2yi is a complex number, which is a vector, and not a mere scalar. So the transition from step 2 to step 3 was really an evaluation of the modulus. If we do not skip any steps, the following should clarify how we got from step 2 to step 3.

|(2x-1)+2yi| \le |(x+1)+yi|

\sqrt{(2x-1)^{2}+(2yi)^{2}} \le \sqrt{(x+1)^{2}+(yi)^{2}}

\sqrt{(2x-1)^{2}+(2yi)^{2}} \le \sqrt{(x+1)^{2}+(yi)^{2}}

(2x-1)^{2}+(2yi)^{2} \le (x+1)^{2}+(yi)^{2}

I do hope this raise awareness for students to treat modulus carefully and question themselves, when they are dealing with a scalar or vector.

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    The Modulus Sign #1Secondary Math
    The Modulus Sign #2Secondary Math