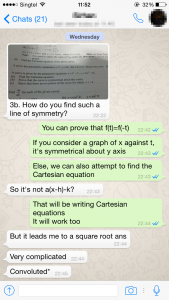
 This question is with regards to parametric equations. We are given
This question is with regards to parametric equations. We are given ![]() and my student have difficulties finding the equation of the line of symmetry.
and my student have difficulties finding the equation of the line of symmetry.
So let us first look at how parametric equations actually work here, since most students are really confused with it. Parametric equations are a set of equations that is “linked” or related using a parameter which is a variable. In this case, both ![]() are connected using a new parameter
are connected using a new parameter ![]() here. And as
here. And as ![]() .
.
Considering that we found the cartesian equation in (i), ![]() , observe that if
, observe that if ![]() then
then ![]() , so for every x-value, we can map to two y-value, the positive and negative one. Thus the line of symmetry will be the x-axis here.
, so for every x-value, we can map to two y-value, the positive and negative one. Thus the line of symmetry will be the x-axis here.
