All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
(ii)
(a)
Required answer ![]()
(b)
![]()
![]()
![]()
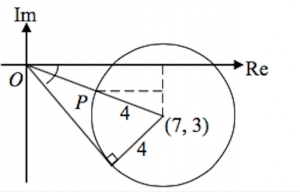
(iii)
![]()
KS Comments:
For (iib), students should draw the right angled triangle out to see what the value is since its required that they leave in exact form. When there is a circle for locus, I usually remind students to always utilise the radius.