All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
(ii)
![]()
![]()
Discriminant of ![]() .
.
Thus, ![]() has no real roots and
has no real roots and ![]() has no other real solutions.
has no other real solutions.
(iii)
Consider ![]()
![]()
(iv)
(v)
![]()
![]()
From (1), ![]() from (ii)
from (ii)
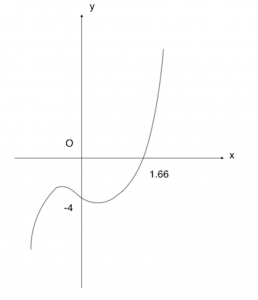
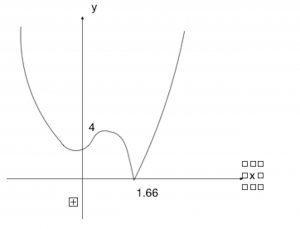
From (2), ![]() using the Graphing Calculator
using the Graphing Calculator
KS Comments:
Sketching of the graph can be done using the GC and since it is one mark, we do not really need to label everything. Students can consider completing the square to solve (ii), or using the quadratic formula to resolve for the complex roots directly. (iii) is a simple replacement and its a “state” question. For (v), students need to note that ![]()

[…] Question 3 (Note Worthy) […]