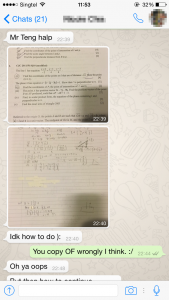
 This questions is on vectors, in particular, finding the shortest distance of a point (0, 0, 3) to the plane. My student was able to do it but had a terrible careless mistake. But nevertheless, I want to share this question as there are a few ways to go about solving it.
This questions is on vectors, in particular, finding the shortest distance of a point (0, 0, 3) to the plane. My student was able to do it but had a terrible careless mistake. But nevertheless, I want to share this question as there are a few ways to go about solving it.
First method will be to consider the vector
And then find the shortest distance using ![]() .
.
Second method is slightly longer which involves finding the foot of perpendicular of (0, 0, 3) to the line. This will require finding the projection vector first.
I personally recommend the first method. As I always discuss in class, students need to appreciate the “golden” triangle for vectors as it can solve everything involving projection and perpendicular distance.
