All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
![]()
![]()
![]()
Equation of tangent: ![]()
![]()
(ii)
Tangent at P: ![]()
Tangent at Q: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Since ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(iii)
Equating the equations of both C and L,
![]()
![]()
![]()
let ![]() ,
,
![]()
Using GC, ![]()
![]()
![]()
![]()
(iv)
![]()
![]()
![]()
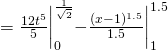
![]()
![]()
![]()
KS Comments:
This question is not difficult. The only problem I noticed is that students were panicking by the time they reached this question, partly due to the heavy weightage of this question. But panicking caused them to make further mistakes.

[…] Question 11 […]
[…] Question 11 […]