All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
![]()
![]()
![]()
![]()
Since ![]() ,
,
![]()
![]()
![]()
![]() where
where ![]()
(ii)
![]()
![]()
![]()
(iii)
![]()
![]()
![]()
![]()
(iv)
Consider ![]() , then
, then ![]()
Let ![]() , so
, so ![]() and
and ![]() , then
, then ![]()
![]()
KS Comments:
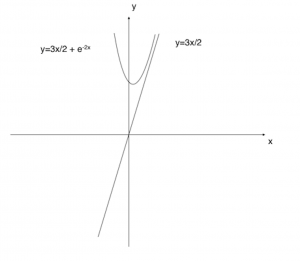
This is fairly good question. The first part explores students’ abilities to relate a 3-variables differential equation. In (iv), they are expected to understand the question first and set the arbitrary constants to the necessary conditions. Don’t forget to use the graphing calculator to draw the graphs!

[…] Question 10 […]
[…] 2013 A-level H2 Mathematics (9740) Suggested Solutions | The Culture on 2013 A-level H2 Mathematics (9740) Paper 1 Question 10 Suggested Solutions […]