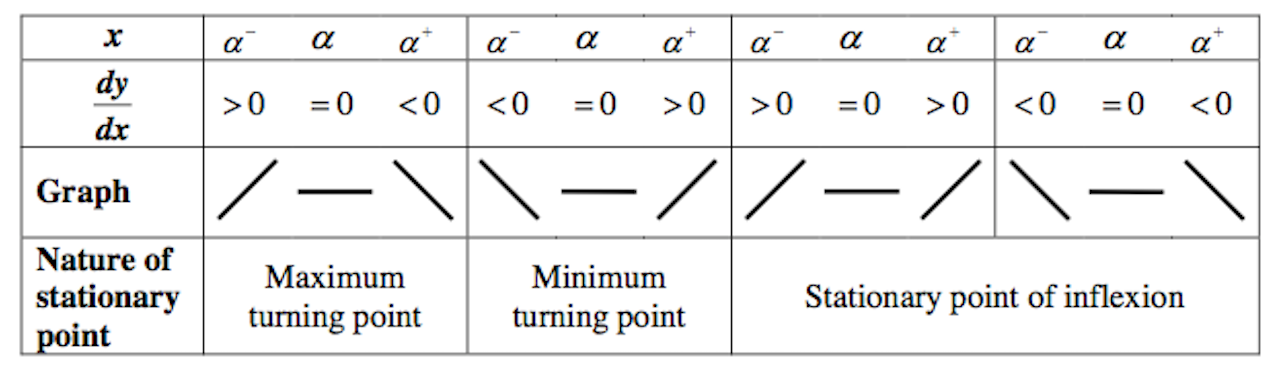
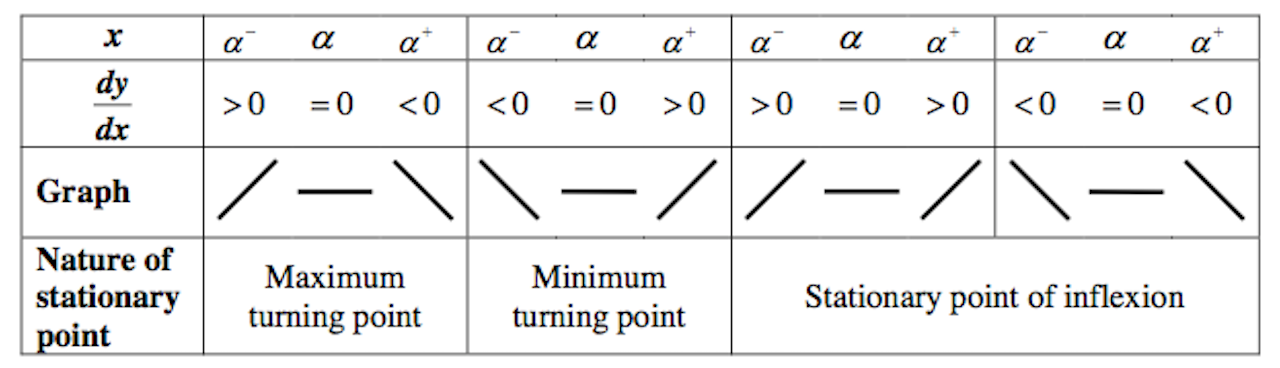
When ![]() , it implies we have a stationary point.
, it implies we have a stationary point.
To determine the nature of the stationary point, we can do either the first derivative test or the second derivative.
The first derivative test:
Students should write the actual values of ![]() and
and ![]() in the table.
in the table.
We use this under these two situations:
1. ![]() is difficult to solve for, that is,
is difficult to solve for, that is, ![]() is tough to be differentiated
is tough to be differentiated
2. ![]()
The second derivative test:
Other things students should take note is concavity and drawing of the derivative graph.