VJC P1 Q9
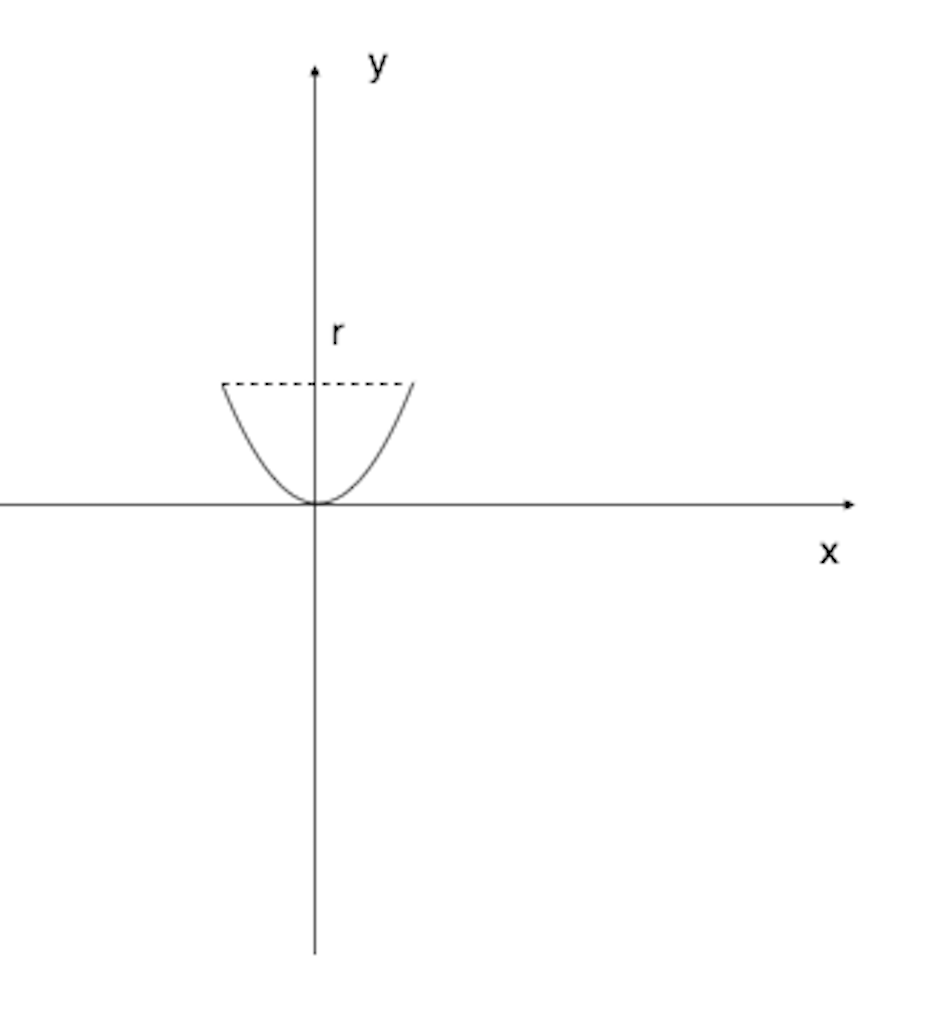
(i) Sketch the graph with equation 
, where 
and 
A hemispherical bowl of fixed radius 
cm is filled with water. Water drains out from a hole at the bottom of the bowl at a constant rate. When the depth of water if 
cm (where 
).
(ii) Use your graph in (i) to show that the volume of water in the bowl is given by 
.
(iii) Find the rate of decrease of the depth of water in the bowl, given that a full bowl of water would become empty in 24 s,
(iv) without any differentiation, determine the slowest rate at which the depth of water is decreasing.
Showing 4 comments
Hi may I know the mark allocation for the sub-parts of this question? Is it possible to include the mark allocation for future questions too?
will try, cos i gave out 2016 prelims to my students and most of these solutions are meant for their independent checking.
Can I also confirm that “y le r” refers to “y is a real number”?
its a typo