All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
Direction vector of 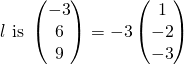
Normal vector of 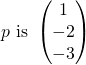
Since ![]() is parallel to the normal vector of
is parallel to the normal vector of ![]() is perpendicular to
is perpendicular to ![]() .
.
(ii)
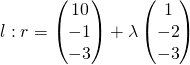
![Rendered by QuickLaTeX.com [\begin{pmatrix}10\\{-1}\\{-3}\end{pmatrix} + \lambda \begin{pmatrix}1\\{-2}\\{-3}\end{pmatrix}] \bullet \begin{pmatrix}1\\{-2}\\{-3}\end{pmatrix} = 0](https://theculture.sg/wp-content/ql-cache/quicklatex.com-d55e54d1894c879a03c77adb14d4172e_l3.png)
![]()
![]()
Point of intersection ![]() .
.
(iii)
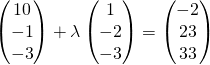
![]() — (1)
— (1)
![]() — (2)
— (2)
![]() — (3)
— (3)
Since ![]() satisfies all 3 equations, A lies on l.
satisfies all 3 equations, A lies on l.
Since ![]() is the midpoint of A & B, by ratio theorem,
is the midpoint of A & B, by ratio theorem,
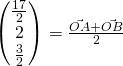
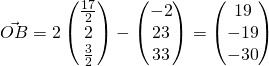
![]()
(iv)
Area
![]()
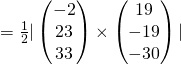
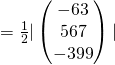
![]()
![]() to the nearest whole number.
to the nearest whole number.
KS Comments:
Students must give answers in coordinates, rather than as a position vector.

[…] 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7 Question 8 Question 9 Question 10 Question […]