So last time we saw STR and here is a quick recap.
- Set the stratification scheme
- Set the stratum design
- Implement the sampling methods for each stratum independently
- Pool the strum estimates to estimate the population parameters
- Estimate their respective variances
- Construct CI, if necessary.
Today, we look at ratio estimation. For starters, we will use SRS only and same as before, we assume there is no non-sampling error, only sampling error.
As usual, we start with the definitions
We introduce two variables ![]() which is an auxiliary variable or subsidiary variable, and
which is an auxiliary variable or subsidiary variable, and ![]() which is a response variable (characteristic of interest). The idea here is to utilise the auxiliary variable which is correlated to the response variable to improve precision.
which is a response variable (characteristic of interest). The idea here is to utilise the auxiliary variable which is correlated to the response variable to improve precision.
Next, we have a new population parameter B (ratio).
![]() where
where ![]() and
and ![]()
And here is the procedure
- We assume
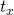 is known,
is known, 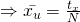 is known
is known - Use SRS and measure
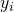 and
and 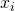 in the sample.
in the sample. - Calculate
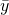 and
and 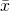 for the sample
for the sample 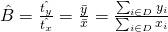
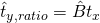
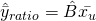
We use ratio estimation because at times, our ratio of interest might be average yield in bushels per acre, ratio of fish caught to the number of hours spend, per capita income, etc. And for most of these cases, the population size N is unknown, so its still necessary for us to estimate a population total. Since we cannot use the estimator ![]() here, we consider another measure of size, that is,
here, we consider another measure of size, that is, ![]() . So we can estimate N by
. So we can estimate N by ![]() . Consequently,
. Consequently, ![]() where
where ![]() estimates the total sample size based on the auxiliary variable.
estimates the total sample size based on the auxiliary variable.
The benefits of using ratio estimation is clear.
- Smaller MSE if x and y are correlated, giving us an increase of precision
- We are able to adjust estimates to reflect known information, and evaluate them more in depth for a more representative result.
- We can adjust for nonresponse.
You might notice that taking a SRS will slight underestimate the true population mean of x‘s, that is, ![]() is smaller than
is smaller than ![]() . And should x and y be positively correlated,
. And should x and y be positively correlated, ![]() may also underestimate
may also underestimate ![]()
Ratio estimation for the population mean ![]() is given by
is given by
![]()
Here we correct the underestimation by expanding ![]() by a factor
by a factor ![]()
After looking at the estimators, as usual, we questions its qualities.
Firstly, the ratio estimators are biased. This arises because the unbiased ![]() is multiplied by
is multiplied by ![]() . The good news is that our variance is reduced, essentially compensating for the presence of bias. This means that although
. The good news is that our variance is reduced, essentially compensating for the presence of bias. This means that although ![]() , the value of
, the value of ![]() for any individual sample is likely to be closer to
for any individual sample is likely to be closer to ![]() than the sample mean
than the sample mean ![]() . Of course, the average deviation
. Of course, the average deviation ![]() , averaged over all possible samples D that could be obtained, is zero.
, averaged over all possible samples D that could be obtained, is zero.
We introduce a population correlation coefficient of x and y first.
![]()
![]()
![]() =
= ![]() =
= ![]() =
= ![]() where
where ![]()
Here, notice that as sample size increased, ![]() decreases. Ignoring FPC, then
decreases. Ignoring FPC, then ![]()
![]() MSE is dominated by the variance. So in large samples,
MSE is dominated by the variance. So in large samples, ![]()
Let ![]() , then
, then ![]() is an unbiased estimator for
is an unbiased estimator for ![]()
When n is large (more than 30), ![]()
Its is worth asking ourselves when this approximate MSE is small. Rewriting it, we have
![]() .
.
So approximate MSE is small when
- Sample size n is small
- sampling fraction
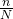 is large
is large - Deviations
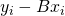 are small
are small - Correlation between x and y is close to
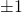
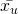 is large.
is large.
Estimated variance, ![]() where
where ![]() =
= ![]() and
and ![]()
When ![]() is unknown, we can substitute it by
is unknown, we can substitute it by ![]() , then
, then
![]()
![]()
Similarly, if the sample sizes are sufficiently large, approximate 95% CIs can be constructed using the standard errors as
![]()
![]()
![]()
For large samples, the effect of bias in the CIs can be ignored.
A distinct advantage of using ratio estimation is that the ![]() iff
iff ![]() . This implies that if the coefficient of variation are approximately equal, then it pays to use ratio estimation when the correlation between x and y is larger than
. This implies that if the coefficient of variation are approximately equal, then it pays to use ratio estimation when the correlation between x and y is larger than ![]()
Next time, we will look at Regression Estimation.
Sampling & Survey #1 – Introduction
Sampling & Survey #2 – Simple Probability Samples
Sampling & Survey #3 – Simple Random Sampling
Sampling & Survey #4 – Qualities of estimator in SRS
Sampling & Survey #5 – Sampling weight, Confidence Interval and sample size in SRS
Sampling & Survey #6 – Systematic Sampling
Sampling & Survey #7 – Stratified Sampling
Sampling & Survey # 8 – Ratio Estimation
Sampling & Survey # 9 – Regression Estimation
Sampling & Survey #10 – Cluster Sampling
Sampling & Survey #11 – Two – Stage Cluster Sampling
Sampling & Survey #12 – Sampling with unequal probabilities (Part 1)
Sampling & Survey #13 – Sampling with unequal probabilities (Part 2)
Sampling & Survey #14 – Nonresponse
