All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
Paper 2
Question 1
(i)
![]()
![]()
![]()
(ii)
![]()
![]()
![]()
![]()
When ![]()
![]()
When ![]() years.
years.
Question 2
(i)
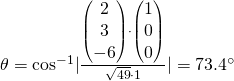
(ii)
Let ![]() be point on L that makes
be point on L that makes ![]() from P.
from P.
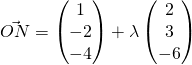 for some
for some ![]()
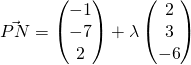
![]()
![]()
![]()
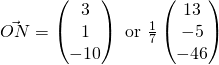
![]()
![]()
![]()
So when ![]() , L is minimum.
, L is minimum.
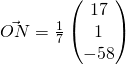
(iii)
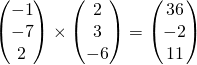
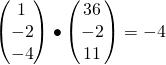
![]()
Question 3
(ai)
![]()
![]() for all
for all ![]()
Since ![]() is increasing function, it has no turning points, f is 1-1, its inverse will exist.
is increasing function, it has no turning points, f is 1-1, its inverse will exist.
(aii)
Let ![]()
![]() Reject
Reject ![]() since
since ![]()
![]()
![]()
(b)
Let ![]()
We need ![]() for all real values of g.
for all real values of g.
![]()
![]()
![]()
![]()
![]()
Question 4
(a)
Let P(n) be the statement ![]()
When n=1, LHS ![]()
RHS ![]()
Since LHS = RHS, P(1) is true.
Assume P(k) is true for some k, ![]()
![]()
Want to show P(k+1) is true, ![]()
LHS
![]()
![]()
![]()
![]()
= RHS
Since P(1) is true, P(k) is true ![]() P(k+1) is true, hence, by Mathematical Induction, P(n) is true for all
P(k+1) is true, hence, by Mathematical Induction, P(n) is true for all ![]()
(bi)
![]()
(bii)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(biii)
![]()
![]()
Least n = 499
Question 5
(i)
Manager is unable to obtain an appropriate sampling frame.
(ii)
Manager can consider taking equal number of respondents from adults and aged first. Then, he can stand outside the supermarket, interview whoever walks in, based on his personal preferences until he obtains the number of respondents he require.
(iii)
As he samples based on his own preferences, there might be selection bias.
Question 6
(i)
Let X denote the number of red sweets in a small packet of 10 sweets.
![]()
![]() (3 SF)
(3 SF)
(ii)
Let Y denote the number of red sweets in a large packet of 100 sweets.
![]()
Since n is large, ![]()
![]() approximately
approximately
![]() by continuity correction
by continuity correction
![]() (3 SF)
(3 SF)
(iii)
Let W denote the number of packets out of 15 packets that contain at least 30 red sweets.
![]()
![]() (3 SF)
(3 SF)
Question 7
(i)
Firstly, the average number of errors per page is constant.
Secondly, the number of errors in a page is independent of the number of errors in another page.
(ii)
Let X denote the number of errors per page.
![]()
![]()
![]()
![]()
![]() (3 SF)
(3 SF)
(iii)
![]()
![]()
![]()
![]()
Using GC, ![]()
Least ![]()
Question 8
Let X denote the mass of pineapple tarts and ![]() denote the population mean mass of pineapple tarts.
denote the population mean mass of pineapple tarts.
![]()
![]()
Unbiased estimate of population mean = 0.8825
![]() (3 SF)
(3 SF)
Under ![]()
Test Statistic, ![]() at 10% level of significance.
at 10% level of significance.
Using GC, p-value ![]()
![]() , do not reject
, do not reject ![]()
There is insufficient evidence at 10% significance level to reject the stall owner’s claim.
Question 9
(i)
![]() since A and B are independent.
since A and B are independent.
![]()
(ii)
![]()
![]()
![]()
![]()
(iii)
If ![]() ,
,
![]()
![]()
![]() (maximum)
(maximum)
If ![]() ,
,
![]()
![]()
![]() (minimum)
(minimum)
![]()
Question 10
(i)
Graph later I plot
(ii)
(a) ![]() (4 DP)
(4 DP)
(b) ![]() (4 DP)
(4 DP)
(c) ![]() (4 DP)
(4 DP)
(iii)
Using GC, ![]()
![]() (3 SF)
(3 SF)
(iv)
![]()
![]() (3 SF)
(3 SF)
Question 11
(i)
Number of ways ![]() ways
ways
(ii)
Number of ways ![]() ways
ways
Side Note: Mr Wee provided a different and interesting perspective here, and suggested that it could be SGECBBAA. I think we both agree that Cambridge isn’t that evil and sneaky. I felt that my nursery rhyme should suffice. Food for thought. 🙂
(iii)
Number of ways ![]() ways
ways
(iv)
Case 1: 2 A’s together and B’s separated
![]()
Case 2: 2 B’s together and A’s separated
![]()
Case 3: 2 A’s together and 2 B’s together
720
Number of ways =10080 – 1800 – 1800 – 720 = 5760 ways
Question 12
(i)
Let X and Y denote the mass of a apple and pear in grams respectively.
![]()
![]()
![]()
![]() (3 SF)
(3 SF)
(ii)
![]()
![]()
![]()
![]() (3 SF)
(3 SF)
(iii)
Let A and B denote the mass of a peeled apple and peeled pear in grams respectively.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3 SF)
(3 SF)
Relevant materials
KS Comments
[…] Paper 2 […]
[…] Paper 2 […]
Leave a Comment


Hi ! Do you have an example of a question with functions n some conics ?
Hi! I tink the ans for 2(ii) should be 1 and 1/3
haha i haven’t check. cos i’m just typing at one go and solving alongside. hold on
Hi mr Teng is 150 for total marks an A? I’m really quite worried now cause I’ve studied so hard
i can’t advise a sufficient grade. That should be good if the curve doesn’t shift. Might be a B though
Omg same scared me for a moment. My part 3 is 36x – 2y + 11z = 4… Dunno if I’m careless or??
OMG mine too! Shit please accept two answers
Oh wait mine is -36x + 2y -11z = 4
Realised I type wrongly.. I got the same as u. Should be correct I think we get diff answer cause we cross product the two column vectors differently. Like we put the direction vector on the other side instead.
I got 1 and 3/7 as well.
I got 1 and 3/7 also haha
Yea I think my part 3 is careless. I tried working backwards but I have no idea how I ended up with those numbers lol
LOL i got 3/7 too
why 1/3?
i got 1 and 3/7 though
Is there e.c.f?
think you forgot to find the point for the shortest distance in 2ii)
yes, that. I totally forgot. i’m doing and typing at the same time lol
Hi~ for 1(ii) how come everything is done in terms of 32-h? my final answer is half of yours. where did i go wrong?
and for 2(ii) i made some mistakes in simplifying the algebra and arrived at 49×2 + 70x + 21 = 0.. how many marks will i lose?
I think you got the equation wrong for qn 1 it’s sqrt. (16 – 0.5h) not (32 – 2h)
i combined to single fraction for ease actually. unless i made careless lol
For 2(i), what if I was careless and wrote sin^-1 instead of cos^-1 but got the rest of the eqn correct? >< Can get 1 pity mark?
Same for 7(iii), if I got the steps leading up to the answer correct but was careless somewhere, will it be 1 or 0 marks?
Thanks for posting the answers!
hi for qn 2ii do you know how many marks is deducted if im unable to find the point that is the closest to P? :/
For Q2.ii) if I managed to get 1 and 3/7 but I got the wrong point cause I subbed in the values wrongly(*bang head*), may I know how many marks will be deducted?
for 4 last part what if i got the least n=499 but my working is wrong because i put the wrong sign? i was careless and i wrote >10^-3 instead of <
Sorry can I ask for hypothesis testing in this paper
If you did the t test but did 2 tail instead of 1
Will u get the entire qn wrong
Hi, you will get 2 marks for the s^2 and miu value.
But you are not alone, I did the same too 🙂
Hi! For the hypothesis testing, if the sign for my H1 is “not equals” (which is the wrong sign), will I still be able to get some marks for finding x bar and variance correctly and state that the test is a T-Test?
For question 3, can I do by differentiation and then equating dy/dx =0?
I scored about 160 for both papers, is this enough to get an A?
Thank you!
i did by differentiation too! is it fine? 🙁
Should be fine cos that’s the otherwise method.
i did the same too hahaha. not really sure if its right because they said ‘algebraic’….
the graph on GC, is imperfect…
http://www.wolframalpha.com/input/?i=y%3D%282%2Bx%29%2F%281-xx%29+graph
hope this helps
Can i use inv sine for Q1ii
I did that too, but ended up with the wrong answer…how generous are they with partial marks? :/
i got this too! but sub into the vector eqn then the answer is different from the answer here. dont know how many marks gone here @.@ the shortest distance one i got a different answer too. sigh…
oops i replied to the wrong comment 😅
no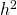 leh. can’t use :/
leh. can’t use :/
I made it to 4 and sqrt(h/2) to get sin-1(sqrt(h/2) /4)
So entire 5 marks gone?
Yes sadly, me too ):
lolol same i only scored 80 for this paper and 83 for paper 1 don’t think its an A
for qn1ii i also did sin inv, but i root the k & let it be ‘x’ is it okay?
cannot you need a square
from what i understand from the comments, changing the expression to 1/(sqrt(4^2-(sqrt(h/2)^2)) also cannot use sin-inverse.. so 5 marks is deducted?
yea, there is no way you can use the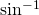 to solve it. :/ sorry. A simple way to convince yourself is to differentiate your result, and you will realise its mistaken.
to solve it. :/ sorry. A simple way to convince yourself is to differentiate your result, and you will realise its mistaken.
wish i had time for that 🙁 thank you
No, because you cannot complete the square! :/
Is lambda = -1 or -1/3 accepted for 2ii? I used instead NP instead
i got this too! but when i use these values to sub into the vector eqn of line L then the answer is different from the answer here. dont know how many marks gone here @.@ the shortest distance one i got a different answer too. sigh
Shouldn’t the answer for 1ii be 11.7?
eh, why? cos I dont think i got careless there.
I think they use sin-1
oh i see. but we can’t use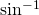 here
here
You’re right! Many of friends got 46.9 years too.
i think because he did it in radians mode (i did that too 🙁 )
Yeah I got 11.7 as well.I integrated directly.
I got 11.7 as well!
for the hypo testing what if my h1 was > 0.9 and my p value is wrong but i did not reject h0 in the end will i lose all the marks?
Hi, for the vectors question, I wrote my points in coordinate form. Will I be marked down? Thanks!
thats fine. no specifications at all
9iii i think is b/w 0.165 and 0.33
hmm, did i consider wrongly? :/ I put , but I didnt really go do
, but I didnt really go do  leh.
leh.
I use 1 – (0.45 + 0.4 – 0.45×0.4) for 0.33 leh
yes 0.33 here too!
Yes I got 0.33 as well; why ah…
omg, accident type extra 3. sorry!
Can the minimum and maximum values in 3ii be found using differentiation?
yea, but must explain why min and max.
If I used 49 lambda^2 -70 lambda +21 for 3(ii) instead will I get marked down even though answer is the same?
Hi, for question 4(b)(iii), shouldn’t the phrase ‘within 10^-3 of the sum to infinity’ be 10^-3 multiply by sum to infinity aka 10^-3 times 1/3?
i am within 20m of your distance, that just means im +- 20m away from u
That’s what I thought of too!
But if you got (ii) correctly, you would have realised -1/2r+3 means that there is only one way you can solve this already!
I got P = 34.8 – 0.147 (h^0.5) for 10iii
ya thats same. haha
ur qn 3b wrong lol
Hey for hypo testing, if i used right tail instead of left tail, but everything else (format test statistics ) same, how many marks gone?
5 marks gone! Because of your wrong direction sadly! 🙁
9iii) I took the intersection between B and C to be 0.1 for the smallest, and 0.3 for the largest (C inside B), does it work?
Yeah that’s what I did also. In the end the largest value I got was 0.365 (different from Mr Teng’s answer) & smallest I got was 0.165. Did you get the same?
Is it possible for the intersection of B and c to be zero? Curious
it can’t. the smallest is 0.1 since that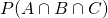 . But this one, I really need to think and draw lol
. But this one, I really need to think and draw lol
Nope I think somewhere towards the end I did something wrongly, my answers’ pretty off :/
For qn 8!, shouldn’t alternative hypothesis be more than since it is ‘-at least’ 😰😰
If it’s at least it means that the shop claims the mass of pineapple is more than 0.9. So if the shopkeepers claim is doubted, means is less than. Yeah the English is tricky…
Hello, thanks for the answer! As for question 10(iv), shouldn’t it be divided by sqrt 3.28 instead? 🙂 since 1 meter = 3.28 feet and h was given in feet
but they want the equation when the height is given in metres.
Yah! I thought need to divide!!
Same here! Cause 1metre is 3.28 feet so if question is in frets then by converting it to metre shouldn’t it be 1/3.28
yea, but they want an equation to estimate pressure when we are given metres. so h is given in meters instead.
But the part above the data already states data given in metres. Doesn’t make sense to change the units for the data while keeping the same numerical value. I think what the question means is that when you take a height given in the table then convert to metres (x3.28), then sub it into the new equation should give the same pressure. So for the new equation should h/3.28 to “convert” back to feet so that the value for pressure will be correct.
oops i mean the part above data states data given in *feet
Sry I think i get it alr
9(ii) should be 0.365 and 9(ii) is 0.065, should be correct
Hi for 10iv can I retype the values of root h in metres in the GC to get a new equation ?
and also 3b I used differentiation to get the min and max points to get the range is that acceptable?
they just want to you to rewrite the equation in (iii), so no need to redo it actually. and yes, differentiation is fine so long as you show the min and max
so means they only accept the rewrite and if retype whole thing in gc to get the new equation is wrong? haha
also for vectors i got the lamda (1 and 3/7 and 5/7) but sub into wrong equation haha is that -3 out of 5?
ya, they specify rewrite from previous part. haha careless, just lose 1 answer mark
how much mark will i lose if i didn’t show the min and max points?
probably 1. cos you can’t really explain how you get the range, without the graph. since its algebraic methods only.
oh ty, that’s a relief 🙂
isn’t it -0.147 instead of 0.147 for 10iii and 10iv?
oh thanks. haha see wrong. age catching up
for qn 9 iii my other alternative was to consider the whole C was inside of B. so in the end i got a value of 0.33 is it logical?
If i write two tail test for the hypothesis testing qn but I got variance and mean correct and i said it’s t-test, can get 3 marks?
2 marks max
3 Marks if you define your H0 and H1 correctly. If not, then only two for your variance and mean calculations.
If u use two tail test h1 probably is wrong though..
For q9iii I used the formula from part ii with P(a’n b’ n c’) = 1- P(a u b u c), then I expanded P(a u b u c) and left all the parts the same except minus P(B n C). For p (B n C) if I equate to zero and sub back to the formula I get. My other value is where C is a part of B so P(b n c) = P(c). I’m not even sure what I’m doing tbh
2ii i think ur 2nd ON got careless/typo, shld be -46 instead of -64
Agree.
And i think the hence method for the shortest distance is the midpoint of the 2 points 🙂
Agree too.
Hi! For the inverse function, can’t I show it using a horizontal line test with a graph drawn?
Yeah should be fine, did the same
for qn 3b i used differenciation to get max and min point, but i didnt get the same values as you did 🙁 is it wrong?
g'(x) = 0 = x^2+4x+1
i got -3.732 and -0.2679 ( i left it in a surd form)
u are right bro
i think 3b should be sqrt(3) -2 and -sqrt(3) -2. check gc
They asking for range boi, sub into g(x) to get y values
use your gc to check pls
Maybe u should be the one looking at your gc more carefully, the values u listed are the X coordinates of the minimum and maximum points of the graph, question asked for RANGE which is the Y values
Hence u need to sub the x values into g(x) in order to obtain the y values.
Nope it’s 1+(sqrt.3)/2 (check minimum) and 1-(sqrt.3)/2
u try sub in those values into the graph in the gc, then come back tell me
Same I got that X too when I used differentiation to find min and max not sure why my Y is so different
Hi can i complete the square for Q2(ii) and show at lumda= 5/7 the distance is minimum
Hi for 9 part ii I think you forgot to plus 0.1 twice? So it should be 0.2 instead of 0.1?
why did u change the answer for 11iv? i got 5760 too 🙁
Same 🙁
yea haha my server crashed and the latex got changed. zz sorry had to retype
Use logic, how can there be more ways with greater a greater restriction
k can
For Qn8, if I got miu and s^2 correct and used ttest but got the p-value wrong, how many marks will I get?
I used one tail test correctly
Probably about 4 marks at most I guess…because wrong p-value will mean your conclusion is invalid.
Hi, my ans for qn 10(ii)a, b , c are different. 10(ii) (a) -0.9670 10(ii)(b) -0.9768 and 10(ii) (c) -0.9953
oh means you’re wrong
Means the subsequent parts all 0 marks ? Or got a few marks
u must have typed ur data wrongly i guess
you might’ve used x on y instead?
thank u so much for the answers!! what about full worked solutions for 12? 🙂
and also what do u estimate will be the mark needed for A grade this time (just a casual estimation will do thank you 🙂 )
the full worked is super long. typing. cos they want to see the mean and variance lol
my guess would be >85 for paper two since most people in my jc(ijc) got>80
how bout p1?
P1 would be >75 i guess
Wah ur school ppl all do so well ah
Paper 1 : 80/100
so low ah 80?
We’ll know the % AB for ijc next year bah…see if this guy is really correct lol
haha, i also quite curious. they dont really release it :/
wow IJC so smart!
95/100 for this paper
You think 50% of Singaporeans scored above 95 for this paper?
he is just trolling or he meant his own mark. haha. that or he forgot the first alphabet of the school. haha
Yeah I got 5760 for 11iv too!
Isnt the answer 5760
Don’t think that the range for A will be as high as 170/200 this year. True enough the papers were relatively manageable like some other years but pushing the bell curve towards a 170/200 seems rather unlikely (it’s just too high). 170/200 requires one to have minimal careless mistakes + be able to do all / most questions which not everyone will pull off so i would say A range is ~160 and not higher
Hi, should 10(iv) be h/3.28 or 3.28h?
but they want the equation when the height is given in metres.
Whats the level of difficulty for this paper ? Haha
Easy. 170/200 to get A
Dont toxic pls
thats a sure A. but not the sufficient mark. 🙂
13,-5,-64 should be -46 🙂
which part?
2 ii), should be -46/7
yes, thanks. typed wrong haha thanks!
sorry i was vague 🙂
Hey for 10iv, I think you got careless cuz you’re supposed to divide by 3.28 instead of times, I.e 1 feet = 1/3.28 m, cuz we were given feet not metre
yea, but they want the equation to be used to estimate when the height is given in metres.
For 3b if I use differentiation method to solve will I be correct??
yea, just need to show min and max points
what is the score for a secure B?
Around 70-80/100
Source?
For qn 3 must the discriminant be more than or equals to 0??? If i put it as more than 0, will i get the whole part wrong??
I think your 11 iv has mistakes haha I got 5760
Hi I got approximately 170 for both papers combined. Is it safe to get an A?
Thanks!
safe unless you forget to count a 10 mark qns that you got wrong
For qn 8 I used ‘does not equal to’ sign instead of <0.9. will I still get method marks for it? The conclusion is the same though.
hi, will i be penalized for 3ii if i never leave my answers in notations? Meaning i leave it as inequalities.
Yeap same her^
They asked for range of g…so I don’t think you will be penalised…but then again it’s functions…so I’m not sure if the markers are gonna be picky or not…
I think for 10(iv) it should be h/3.28 rather than 3.28h
but they want the equation when the height is given in metres.
For qn 10iv) in the square root is it supposed to be (1/3.28) ?
Yes, I think so too!
Yeah, I think he is wrong. Should be divide instead of times.
but they want the equation when the height is given in metres.
I same as y’all but like another tuition website did times instead of divide like us
Quite sure divide is correct. But doesn’t matter to me because I carelessly divided the 34.8 as well LOL hope after subtracting all my careless marks still can get A
cos they want the equation used to estimate P when h is given in metres.
1 metre = 3.28 feet so 1 feet = 1/3.28 metres
“when the height is given in metres” means for any given height in metres and not the same value in the table now representing height in metres right? sry idk how to phrase clearly
Mr Teng is right.
For example,
if h(in metre) = 1, then h(in feet) = 3.28 feet.
if h(in metre) = 2, then h(in feet) = 6.56 feet and so on.
So the equation should be P = a(3.28h) + b.
And yes, I got this wrong too. I made the same mistake of dividing 3.28 instead of multiplying.
How much do u think is needed to get an A?? As in for both paper 1 and paper 2 together. 🙂
170/200 minimum score
So high?? Are u serious?? Was the paper that easy??
stop scaring people
170 is just confirmed and sure and safe. but you dont need that much. I can’t really filter the trolls here entirely, its too much to read. But i’ll say 160 is a good number to work with. 155 is optimistic.
From what i gathered from my band 3 classmates and friends, they found the paper easy, moreover, i hear stories of my seniors getting 70-80 marks and not getting their A. Believe it or not, u will find out next years during the release of the results!! I am serious..
2013 was a difficult p1 and easy p2 too. I had seniors who got around 70+ after both papers with A. So the minimum bar isn’t that high. 170 probably will get A but whoever says it’s the minimum mark required is pulling those numbers out of a hat…
hi i careless wrote Y = -0.147x + 34.8 and y=-0.266x+34.8 for(iii) and (iv) will i get some marks?
Answer is No, because they want it in terms of h and P.
you need to follow their variables. sorry.
Would I get an A if i scored around 150?
90% chance! very likely
No, u need to get 170 and above
@hi there, can u provide proof of your claims? 🙂
LOL as if u’re from Cambridge. pretty sure last year’s A range was lower than 170/200 & this year’s papers are harder.
Hi can u post a rough estimation of the range of marks to get A,B,C and D? Thank you very much (:
is 160/200 enough for A? and how many marks would i get for hypo testing if i got the unbiased estimates, t test and conclusion correct but i did right-tailed test so i was wrong
wrong test whole question wrong sorry bro
U need 170/200 to get A
Hi hope u get B fearmonger dog
Yes due to how easy the paper was, i also think u need 170/200 to get A
lol dont be nasty its true my ijc friends got >80 for paper 2 even those who scored C and D during prelims
I guess the hardwork paid off 🙂 Good job
good job ijc you did yourself proud! what a remarkable achievement! do you feel better sharing with the world how amazing your math abilities are?
I think you need to state them clearly, so it really depends on how extensive you showed.
ya la, should can. 🙂 its enough. And you will get marks for your estimates, 2 since they ask for it. Your test, however, might lose like 3 – 4.
if i didnt explicity state the mean and variance, will i lose alot of marks? i still got write X~N tho
you need to, cos its the first line of the question. :/ So you need to state explicitly ANY normal distribution you use.
if i state X~N(mean for the qn, variance for the qn) then is it okay!!!
and i wrote out the calculations but its something like X~(5X300, 5X20^2)
Think this might be fine. 🙂 cos they just want to see the calculation. I’m just being really explicitly above, in case.
How many marks lost if didn’t write
Hi i wrote P=-0.147h +34.8 and P=-0.266h+34.8 instead of the rt h. Will i get any marks?
Answer is no because they asked explicitly which one was the best model, so they assumed you pick the wrong choice. :/
i made the same mistake but i wrote that using part 3 since r is closer to -1, y=-0.147x+34.8
Yours is even worse! You will have no marks because you didn’t put in terms of h and P!
wah then 5 marks down the drain?
Hi what’s the estimated A grade range overall?
170/200 and above to get A
>160 ba
I typed n =10 instead of n=8 into my GC for the hypo testing qn… And so my p value etc all wrong. How much marks will I lose? 🙁
You will lose 4 marks I guess…provided your H0 and H1 is correct.
What can be the range for b and c grades
A is >80 B is >70 while C is >60
Where do u get your mark range from?
yeah hes right my seniors who got 80
Are you xu jie?
Lol that’s not true
Troll… Mark range is usually the same unless the paper is insane for that year ie 2014. This time it’s milder so it should be around the standard range.
What’s the standard range for A?
He is right, the paper this year is actually alot easier than 2014, so the range he gave is logical due to moderation.
yeah I have seniors who got >70 last year got a B so hes correct
Its harsh but learn to accept it, sometimes we do not get the things we want in life, and most importantly a levels is not everything.
60-70 for C
70-85 for B
Go back to the O Level e math forum. You’re drunk 🙂
He is actually right because my schoolmates also felt the paper was easy. I amfrom a bottom jc btw
Exactly why your friends found it easy 🙂
Yes, they are band 3 in the maths banding btw, and if they found the paper easy, why wont u? Anyway i apologise for being harsh here.
Why 1st qn cannot do sin inverse? I dont see anything wrong cos I do 16 so 4^2 and the other h/2 sqrt……? Ans I think same
no, its different. you can try to do a proper substitution and check your answers.
hi, for question 12i, it’s not P (5X > 1600)???
they want 5 independent apples, not 5 times an apple.
Does anyone know if Cambridge gives full ecf? Or do they minus the answer mark for subsequent parts?
No ecf only method and answer mark
Hi if 3b I did not put greater or equal to for the sign how much marks would I get? Cus the answer is the same
Is it really a must to write E(X)=…… ,Etc
Cos I just wrote like
X~N( ___,____)
Yea, you need since they put it in the first line.
How many marks will I lose if I didn’t..
yeah i also wondering… mr teng can ans? 🙂
1 mark
Yea, u just lost 2 marks for not doing so
For 12iv) if I carelessly wrote 0.95X instead of 0.85X and hence stated the wrong expectation and variance without working showing how I got the ex and var, will I still get any marks for the question? Thanks.
Anyone got 5040 for 11iv?
maybe, you can share your method. I might have overlooked a case too haha
My method was just (4!x5x4x7x6)/(2!x2!)
Cant spot the loophole though
Hi, for the hypothesis testing question, how many marks would I lose if I concluded wrongly but got the p value correct?
lol wtf the conclusion is the most important part you might get the whole qns wrong if cambridge were strict or else its -1
2 marks gone
2 Marks…1 for saying you rejected and 1 Mark for the conclusion based on this evidence.
This paper is harder than past years’ papers right?
Was way easier than other years, would say 170/200 for A
If you are thinking this year’s paper is difficult, you should be worried, because I felt both papers were manageable.
Yes agreed this year papers were easy
Ya la u guys very pro mah. We are just the average student and we found it difficult. If u guys found it easy it’s ur opinion. Majority of us found it slightly tougher than last few years. And no one can predict bellcurve. It’s best to just concentrate on your other papers. These jokers can go ahead and predict the bellcurve cos it’s based on their marks, not the entire cohort. Even if a prediction is done based on one’s own school then it’ll still be unreliable because there are about 18 JCs in Singapore, considering also the private candidates and what not. Don’t heed their so called “bellcurve range” cos the probability of it being that would probably be close to 0, just like their EQ.
What i based on is what i gathered from my band 3 classmates and friends coz they found the paper easy too. And my teacher also told me many stories of my seniors getting 160/200 and still getting a B. Anyway, this is just my take, believe it or not, u will find out during the release of the results next year.
i feel you mate
Yeah I am one of them I got a B even tho i scored >80 for p1 and >70 for p2 last year
For qn 3b, I excluded 0 from the range because the rhs of curve tended towards zero. Got stunned when I saw it so I just excluded zero..
Hi for question 9iii, for greatest value I took P( B intersect C) as 0, and for smallest value, I took that B as a full subset of C, is that correct?
Hi, for the probability question I got 0.285 as the greatest value and 0.165 as the least
Same
Thank you Mr Teng for the answers!
I would like to ask if:
• Q1ii: integrating wrongly (sin inverse) will warrant -5 completely
• Q12ii: I carelessly calculated variance wrongly by using 20^2 for both, does that also mean -3 completely? I wrote out the steps to get the distribution though!
Thank you so much in advance 🙂
Although I’m not Mr. Teng, maybe I can help answer you:
Q1ii Yes, all 5 marks will be gone because you started off wrongly.
Q12ii You may still get 1 mark from your calculations for E(Whatever your wrote here).
Hope that will clarify! 🙂
For 10iv, I did 10080-(7!+7!-720)=720
Where did I go wrong?
You got to perform a division of 2! when calculating the case when 2 As are adjacent but not 2 Bs. I made this mistake too 😛
if i state X~N(mean for the qn, variance for the qn) then is it okay!!! and i did my calculations same as u but inside the brackets and never put E(x). If not how many marks lost?
Hi, for Q3(b) If I did by differentiation but didn’t have time to finish subbing in the x values to get y, how many marks would I get?
Oh and also for Q1(ii), why wouldn’t sin-1 work, and why must it be ‘complete square?’
Hi! For question 2(ii), can I calculate the mid-point between the two points which are square root 33 from point P? Thanks!
Hello! May I know what is the minimum marks that I have to get in order to score a B? (:
70-85 marks for B
yeah right …
Hi Mr Teng, for the hypothesis question I did a 1 tailed z test.. How many marks gone ah?
wrong test is zero sadly
If you got mean, population variance, H0 and H1 correctly, then 3 marks at most. Won’t be zero! Don’t worry! 🙂
Zero marks
dont know if you’re serious or trolling. finding unbiased estimates min. 2 marks. plus define H0 and H1 one mark.
For ques 4bii I carelessly wrote >10^3 so I got 498 instead. Will I get a zero??
By standard range, do you mean by
A grade>150
B grade>120 etc?
Its actually 170/200 for A, 140/200 for B and 120/200 for C
Yes hes right
Hi~ for 3aii will i be penalised if i didnt put the +- after square rooting and just used the positive square root?
Yes…you will be penalised! 🙁
will i get ecf if my h0 and h1 is wrong but the rest i did accordingly?
normally for hypo theres no ecf sadly, bcos i made the same mistake as you during prelims and got 0
Cambridge might have different marking style lol
No…once H0 and H1 is wrong…whole thing goes down the drain sadly! 🙁
is 150 for both papers an A?
No u need 170/200 and above
RT^
RT^
He is right considering how easy the paper is this year
But only two of u guys are saying it’s easy? Ever wondered what the majority is saying? Stop being so delusional
How are you so sure about that?
From what i gathered from my band 3 classmates and friends, they found the paper easy, moreover, i hear stories of my seniors getting 70-80 marks and not getting their A. Believe it or not, u will find out next years during the release of the results!!
Yea yea yea band 3 band 3 band 3 classmates you can stop repeating your shit in every single post -.-
No u need 170/200 and above to get A
agreed. I really dont think >85 to get A though. Maybe 80, but even that’s a stretch. I’d say 75 has fair bit of hope. But oh well, if 75 still cannot get A, I think we’ve all tried our best.
best comment i’ve read here haha thanks man
ya, 85 is like confirmed safe sure A. 80, will be entirely dependent on how well some schools do, At the end of the day, given math is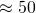 distinction and consider there are 18,000 (roughly) candidates, there are 9,000 A’s to go around. of course, some school tend to take more than proportion haha. But 80 is feasible tbh, if you look at it as 160/200, it doesn’t sound too hard. There are two papers after all haha 75 will be a nice number that many will benefit from, but if too many benefit from it being 75, it might just tip to 76, etc. You need to be in the median to be safe.
distinction and consider there are 18,000 (roughly) candidates, there are 9,000 A’s to go around. of course, some school tend to take more than proportion haha. But 80 is feasible tbh, if you look at it as 160/200, it doesn’t sound too hard. There are two papers after all haha 75 will be a nice number that many will benefit from, but if too many benefit from it being 75, it might just tip to 76, etc. You need to be in the median to be safe.
this is just my opinions la after seeing bell curve in universities, etc.
What about the proportion of Bs received? Is it around 70-75?
they never say anything about B’s can’t be 70% if A’s is 50 %…
haha oops I meant to ask if the range of marks of 70-75 is safe enough to secure a B?
yup, thats very safe la haha
Hi!May I know how are method marks allocated?
for question?
Like in general do they award u method marks if your method is right but maybe u sub in a wrong value due to carelessness?
Can i know how method marks and ecf are allocated for 10iii and 10iv?
you mean, like if your r values are mistaken? if you use the correct method to convert, should get 1 for iv while 1 for iii since your probably picked the wrong model.
I mean if i pick the correct model but sub in wrong values in the calculator. How many marks will i get??
Depends on the cohort performance. Normally they award method marks generously if the whole cohort did badly for that particular question.
in general, yes.
Is 152 safe enuf for an A? Provided that i didnt minus off some method mark that i am unsure whether i will get?
if 10iii is wrong do i get ecf to 10iv?
Is it safe to get an A with 152? Provided that i minus off the working marks for questions tgat i am ubsure whether i will get any working marks
if thats so, should be okay. low A perhaps if all is well.
you should get method mark.
Hi Mr Teng, then what is minimum marks required to get a B (/200) for this year’s paper? I am really confused right now due to the trolls. Thank you very much!
I can’t really advise a sufficient grade. There are a lot of them, finding this paper more than manageable. Perhaps, >135?
I see, thank you! (:
thanks a lot for this genuine comment. all the best for your next papers.
I don’t understand if for every year the standard difficulty level is the almost unchanged and many can score 170+, why don’t Cambridge just officially raise score for A to be 85% since it’s what A really means? I don’t think they will raise A by 15+ marks just because people are competitive, because this is penalising the whole batch of people just because they all generally more capable?Bell curve is used to standardise grade when the paper difficulty level fluctuates so much that it cannot represent ABCD fairly. This year’s paper is neither too easy or too hard, why would they change their official standard? Lastly, the estimates of out scores are not always accurate and usually we get worse than we think. So how would your senior gauge their scores, even they are unsure how would u be so sure? Simple example is we got people who think they get 170+ and eventually got B and people who think they got 140+ and got an A. Please don’t do this to affect candidates’ mood at this point of time, PRO 🙂
From what i gathered from my band 3 classmates and friends, they found the paper easy, moreover, i hear stories of my seniors getting 70-80 marks and not getting their A. Believe it or not, u will find out next years during the release of the results!! Anyway moderation is to not to benefit us but limit the number of As.
Shut the f up. Stop it with your band 3s and stop demoralizing people. U can get good marks then good for you
Lol chill, he is just giving his honest opinion… But, its sad that most of us here just only want to hear good stuff.
Yeah heres some good news my senior got A even though she got ~60 for both papers. Its your choice to believe me or not
For qn 10 , the ans is the third graph? But the scatter diagram itself already shows a non linear relationship….
but they suggest we consider the r value found in (ii).
Roughly what’s the min score to get B :/
140/200 minimum to get B
>140 minimum this year
Hi does anyone know the range of values for a B grade? Is it really as high as minimum above 70? Did quite badly and had a lot of careless. Barely above 60 overall 🙁
Yes…considering how easy the papers was I would say a minimum B will be 140.
Minimum B is 140/200
Like for example, H0 and H1 is wrong, my unbiased estimates are right and i mentioned under H0, T~______ but due to my wrong H0 AND H1 my p value is wrong but i still managed to conclude correctly, will i get 3-4 marks? Appreciate a truthful reply.
2 marks max.wrong test the whole question is gone my friend
Hey i got roughly 65 for paper 1 and 60 for paper 2, would that suffice to get a B grade? or would i have to settle for a C?
You might have a chance of getting B but be mentally prepared next year
I think you may fall into the low B high C range….so you do have to be mentally prepared…
how do u think ard 75 for paper 1 and 69 for paper 2 will fare? i didnt take into account method marks and all… i know its’s low chance of A but is it enough for a guaranteed B?
it should be at least B la. For A, can still hope for it since you have method marks 🙂
Isn’t the usual standard range for math ard 75-78? Why is this year’s range higher? Isn’t The paper ard year 2013’s standard…
If you ask me its actually easiest compared to the other years papers
but no one is asking you..keep your delusions elsewhere. 🙂
yea, you can put it that way. but 75-78 isn’t safe, a little movement can change a lot. :/ This year paper actually not that hard, hard-working ones might be well rewarded as they are a handful of tutorial level questions. haha marks mostly lost due to carelessness or misreading.
how bout lets say 162?
sounds bout right. maybe can go 1-2 marks lower. haha really depends on friends in Bishan and along Bukit timah Road.
from bukit timah here. heard lots of people sighing during the paper. it wasn’t super difficult like internal papers but it definitely wasn’t “one of the easiest papers” either.
Another student from Bukit Timah. Paper wasn’t that easy but there were talented individuals like John Loh who got close to full marks so average would be higher thanks to him
Hey but friends from bukit batok(MI) found it relatively easy scoring >70
From Bukit Timah too. Somehow my peers and I found it harder than the trolls above lol
you said they are trolls alr. dont worry. statistically speaking, if you’re from bishan or bukit timah, you are safer.
hey.. i got about high 50+ total… is my B/C totally gone? 🙁 would appreciate some help.
Can’t really say la, it depends on how many “tanking” the bell curve too. :/ But this year’s paper isn’t that difficult. It has a few tough questions but they amount to probably 10-15 marks for both papers actually.
hi~ may i know what is the 0.145 that u add in 9ii?
try drawing out everything, you can find all the numerical for all the spaces alr. then just substitute according. 0.145 should be one of the spaces. 🙂
will i get method mark for 1 – P(AUBUC)??
my answer was 177/1000. i used A + B + C minus (AnB + AnC + AnB – 2(A × B × C))
the 2(A ×B × C) is for the overlapping of the ABC.. is this very wrong??
Hello! If i cannot prove the MI that LHS = RHS but managed to do prove p1 and do up to stating pk and pk+1 how many marks out of 6 would i get?
probably lose 2-3
Hi, 76 for Paper 1 and 83 for paper 2, will it suffice for an overall A? 🙁
should be bordering there. just pray to bell curve god
What about the proportion of Bs received? Is it around 70-75?
Hi! If I used the z-test instead of t-test, but the conclusion is still the same. How many marks can I get? 🙂
And for question 9, why is the greatest value 0.33?
Thanks!!
you should still get marks for the unbiased estimates, 2. and your test if you set it up right with h0 and h1, along with the variables denoted, 2. then the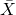 distribution. but you should lose 2-3 marks from the test stat error,
distribution. but you should lose 2-3 marks from the test stat error,
for question 10, how much can I get if I reversed the x and y variables? like y axis is square root h while x axis is P
Sorry, no marks can be obtained as you mixed the up! 🙁
yea, you can’t they already said the model to measure pressure at different heights. so even without physics knowledge, you need P on h
well shoot :/ what about question 11 part 3 if i wrote 6! divided by 2!2!, will I at least retain 1 mark for the 6!?
Hello! I’m from RJ and I can safely say the average in my school is about 160 or so, so please don’t listen to the trolls above saying that it’s “so easy”, because while the paper wasn’t conceptually difficult, a lot of us aren’t very well trained in spotting careless mistakes and fall prey to them!
I myself scored about 166, and I’m fairly confident that it should bag me an A. Mr Teng, please tell me if this trust is misplaced.
yup thats pretty safe haha i think >160 is quite safe. Ya I dont know how to remove their comments lol. and yes I think the whole paper is like careless, like i told some students, you guys just bled marks without knowing, cos the paper was indeed very sneaky haha
So true. Made a lot of slips here and there and they are all avoidable. *sighs*
haha yea, quite wasted actually. if you look back and do it, its manageable. but oh wells, its over. and thanks for helping me explain with the regression L)
You know if you were to analyse the “trolls” comments, it seems like it’s from the same person. All the trolls had the exact same bellcurve range and also called themselves from the lower tier schools. So people, just be a little discerning when u come across comments like this. Their predictions are off the charts! 170/200 for a paper with about 20m difficult qns and not forgetting the careless mistakes that cannot avoided by anyone, I’m sure it’s overstated. Best right now is to place ur hopes on other papers and try to get ur desired grades in them and not waste your time on these trolls (or maybe just one troll with multiple accounts). All the best for the remaining As people!
haha i just ignore them. lol and i think difficult questions not till 20m so much la, but careless, a few of my better ones also made some careless here and there. :/ the paper was sneaky. 170/200 is just like a very secure and safe A, overestimation, yes, but its like guaranteed and should not be confused with sufficient mark. And yes, next week is one hell of a week. All the best!
Hello!!! May i know what is wrong for my method for q10iv? I did this instead:
4! × 5p4 /2!×2!
So i slotted the 2 As and 2 Bs in between C G E S using 5P4 : _C_G_E_S_ (and arranged these letters by 4!) Then i divided by 2!×2! Because the 2 As and 2 Bs are the same so my answer is 720.
U didnt consider quite a lot of cases. Ie like when AB are together ie ABCGABES ; do note AB can switch postion to BA.
Also didnt consider like ABABCGES etc
Can I get a B or C for 126/200?? I am so nervous!!!
That’s very good chance of an A already. I am 100% sure you’ll get that A
I am so nervous and please tell me can I get a B or C for my math if I get 126/200???
Please tell me can I still get above C if I get 126/200??? I am super nervous now.
can la. dont worry so much 🙂
Most probably a C, but C is not bad, considering that most students get B. But anyways, good luck and dont think so much, a levels is not everything in life.
Yes, I do agree A’levels not the end of world haha. And you have more papers ahead! 🙂
I got around ~140 and still got my A last year no worries
Is it possible to get marks if I forgot to round off for 4dp for the question that asked to find the r value?
oh, i think since the marks are bundled to 3m. so the rounding off probably carries 1mark. I might be wrong though and it could be harsh and each 4 dp is an answer mark.
86/100 for Paper 1 and 78/100 for Paper 2.. Got chance for A?
yup, definitely pls. but how come paper 2 lower than paper 1 haha. but good job 🙂
For 12iii
If i only changed the expectation but i forgot to change the variance am i going to be awarded any marks?
i doubt it, unless you actually showed the distribution for the prices.
For question 2ii
If i did not find the closest point of L to P but i am correct for the points in L, how many marks did i get penalised?
yea, i forgot that part too while typing it haha its a hence part, so it should be just 2m
Hey Sir,
I got around 72 for P1 and 85 for P2 got A chance?
(Pls dont answer “Pro” and “Hi there” who i trying to exert that min A is 170)
yes, definitely 🙂
but it’s a low chance right? 🙁
78, yea is bordering lo. considering the difficulty of the paper. but should have a good chance la
If use right tail test but p value is still greater than 0.1, which means conclusion will still remain as not rejecting Ho, will I still get 0 for the entire question?
if you set the test stat etc right, you should still get a mark or 2. 🙂 plus they should award 2 marks for the unbiased estimates.. unless you never find
I did find the unbiased estimate for population mean and variance.. I wrote everything correct except I wrote right tail test instead of left tail test.. Which means only my p value and H1 is different but the rest are all the same.. May I know how much would I get in this case?
the estimates are 2m. did you use T test? and say 2-4
50/100 can get C? :/
For qns 10iv) Is it possible to change h from feet to metres in GC? And then use the new equation provided by GC.. Can we use this way?
they told you to rewrite (ii) alr. so you aren’t expected to linear regress again. cos this will change the data set actually. :/
For question 2(ii), my lamda is -1 and -3/7 because I use NP instead of PN is it correct?
doesn’t matter, so long as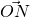 is same.
is same.
ohh but my final answer for ON would be (-1,-5,2) and (1/7, -23/7, -10/7) instead of the given ans. is it alright?
should be the same. did you take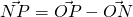
Yup I did that but my answer for ON is not the same
i got this toooooo!!!!! pls tell me it’s accepted ;(((
if you put these ON in to find NP, you dont get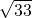
i think we made the same mistake 😧 if im not wrong, u wrote 49x^2 + 70x + 21 = 0 instead of negative 70x. cuz thats the mistake i made i think.. using negative 70x will get u the right answers with no negative sign.
Will there be 1 mark for writing 1-P(A U B U C) for 9 part ii?
dont think so. but lets hope, cos I never see marking scheme
Hi I got around 150 in total. What are my chances for A and B?
for q1ii) i flipped dh/dt around to get dt/dh so i can integrate wrt h but i forgot to divide by half for the expression when power is raised to 1/2 from -1/2. so my final answer was half of the correct answer. do i get method marks for finding the C in my eqn? or is it a total loss of 5 marks?
you should get 1 🙂
If I got s^2 and mean and null with alt correct but used the wrong test but with a correct conclusion as it is the same as t-test will I get more than 3?
probably mins 2-3.
Hi please be honest with me!!
I got around 79 for p1 and around 75(may go down cos im unsure about sampling) for paper2
Am i still able to get an A??? 🙁
shouldn’t answer for 3(b) be R\(0, 1+rt3 / 2] ? When you use GC to plot, the left side of the graph tends to 0. Which makes sense since y=0 is an asymptote of such a function.
the left side has a turning point actually. haha
oh right… haha sorry
the right side leh? tends to 0 so how ah?
http://www.wolframalpha.com/input/?i=y%3D%282%2Bx%29%2F%281-xx%29+graph
this is the graph. and yes, as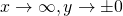 since y=0 is an asymptote. but since the graph still cuts y=0 when x = -2, its still part of its range.
since y=0 is an asymptote. but since the graph still cuts y=0 when x = -2, its still part of its range.
Ah I get it! Okay so how many marks will be deducted if I exclude zero? I found the min and max points but I didn’t rationalise it. Hahha it’s a 5m qn. I hope it’s just 2m cos I managed to find the max and min points correctly but I found it time consuming to rationalise.
you should lose the answer mark, so maybe 1-2 since they also want in simplest form.
Hi, I wrote H0>=0.9 instead of H0=0.9, the rest was all the same. How many marks will I lose? Thanks!
Do you know roughly how many marks will I lose? :((
assuming you found both the estimates, will get 2 marks, t test performed correctly and correct p should be 2-3 marks.
Q12. For var I used 5^2var(x). And similarly for all var. Am I completely wrong? Or do I get any sort of marks for calculating the probability with the wrong distribution?
ya, thats wrong. :/ Might just get 1 mark here and there.
Hi for the poisson qn
Can we say the errors that occur on a page are random
For one the reason to be modeled as poisson
sure. 🙂
Hi, for 1(ii), if I integrated wrongly and did it to the power to 3/2 instead of 1/2, will I lose all the marks?
yes :/
Holy cow same mistake as I did! So freaking careless, 5 marks gone like this……
the graph can just draw on the full scrap paper, they say draw not stretch so i a bit scared
ya, can just draw. haha its 1 mark…
to the trolls, karma will get you. engage in fear mongering somemore, you will get slapped and wait next year you’re gonna screw up your own results. 🙂 to everyone else, let us focus on our upcoming papers.
haha. all the best for the other papers. 🙂 I’ve trashed most of them alr.
Hi, thank Mr Teng for your answer:))
Just want to ask about my careless mistakes
For function question, I got X values and Y values, but I just forgot to write out the range, how do they penalise?
For the very last Q12, I forgot to time 5&8 to find variances, but the individual variable I got time 0.85^2 and 0.9^2, might lose 2 marks maybe?
For probability question last one, my method is exactly the same as yours (consider three cases), but for second and third case I got wrong, would I just get a 0?
Please answer me Mr Teng😿
you mean, you differentiate? then need to show min and max too. probably lose 1 for the answer mark and 1 more, depending if they are stringent with you supporting your answers with regards to min/max points.
yea, bout 2 marks.
nope, you still get marks for the case, probably 2m if optimistic. You won’t just get zero. cos there are method marks.
Will 1 mark be awarded for correct definition of the Let X denote….. ie X~Po(7.8) variable in 7ii? I saw wrongly and calculated for X more than or equals to 10.
Yes…given that the question is worth 3 marks…you probably will have 1 mark. 🙂
eh, not really. :/
Hey Mr Teng I think my comment wasn’t sent previously, if I got the idea for qn 9 that the smallest intercept is 0.1 while largest intercept is 0.3 (C inside B), but my final calculation had some error resulting in wrong answers, do I get 1/2 marks? Thanks!!
math paper, no 0.5 marks. :/ sorry
As in 1 or 2 marks haha
oh haha so sorry. hmm, that depends on your explanation. I would think they give 2 for the min and 2 for the max. So if your explanation is sound and logical, you should get the marks. 🙂
Mr Teng what do you think about 150/200 for math? 🙁
thats good. Can get A if all is well. 🙂 Don’t worry too much.
Mr Teng what do you think about 150/200 for A? 🙁
Hello Mr Teng. If for hypothesis testing I did everything correctly but used the wrong value for unbiased estimate of variance how much will I be penalised?
the estimates, should each be a mark. if you got them right, then ok. if the test is right (h1, t-test and all), your p will be wrong still since you used the wrong estimate and this should cost you a mark. i’ll say minus 2-3.
Alright thank you!
Oops haha sorry by 70-75 I meant the marks for each paper
Oops haha sorry by 70-75 I meant to ask if that range for both papers is safe enough to secure a B? And is it possible to get an A? I understand that the chances of securing an A might be low?
You will have a high chance if you used the correct method but got the wrong answer rather than leaving the whole question blank or used the wrong method. NO worries I got my A despite getting ~140 i guess method marks helped me to ge that A
Thank you for easing my worries ^^
Hi my ho I wrote greater/equals cause they said at least.. And my h1 and the rest is the same, how will I get oenalised. and can you show the max min method? Cause I’m quite sure I differentiated correctly and prove min/max but my answers seem different thanks!
you can’t write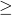 for h0 as thats quite a different test. You might lose 2 for that if all else is good.
for h0 as thats quite a different test. You might lose 2 for that if all else is good.
let
when
Here, and you can figure the other one other haha. Its too much work. :/ and you need to show which is min or max too.
Thanks so much!
pleasure. all the best 🙂
Hello! 🙂
For the range of g, i found the two values for x at stationary points, but i only calculated one … (i thought the other side y had a max value of zero looking at gc) How many marks would i be awarded for that? :/
Hello Mr Teng. If for hypothesis testing I did everything correctly but used the wrong value for unbiased estimate of variance, how much will I be penalised?
for question 11 part 3, will I at least get 1 mark for writing 6! when my answer is 6! divided by 2!2!
this 1 mark is very important to me ;_;
For 2iii, can I leave it as -36x+2y-11z=4?
haha why not?
(Y)
And to all users, good luck for the remaining papers. Hopefully we will prevail : )
Hi Mr Teng,
I used the critical region method for hypothesis testing, but I used a right tail test instead =/ But my test statistic and everything else is right except the H1 and conclusion, how many marks will I get?
you might just lose 3-4 marks. cos if the estimates are correct, you will get 2 marks for them too. 🙂 they did say find them
Sorry to disturb, for the possion inequality qns,
I put as P(X=0)+P(X=1)<0.05 and i used gc to solve for n is 4. Am i able to get full credit? Considering i kind ofwrite down the formula for the poisson thing and then cancel it
you need to write the formula cos they want an inequality in terms of n
Hi Mr Teng!
Thank you so much for doing this 🙂
May I know whether you will be providing the answers for the H3 paper?
nope haha, i’ll be overseas during that week, i have other commitments. sorry
For 6ii I cc-ed wrongly put 30.5 instead do I still get marks? and this will affect 6iii also do i get marks for 6iii?
eh, no, cc wrong means wrong haha, but you lose just lose the method mark. not the entire aprroximation. math is all method marks, not exactly ecf
oh but i do still get marks for the distribution and approx for 6ii right? just the answer and 6iii wrong
also, for the p n c question last part, I used 10080 -720 – 4032×2, although the 4032×2 part is wrong do i still the “-720” part right and get marks?
If I didn’t show my calculations for Q12 parameters , how many marks will be deducted
May I know why we can’t use horizontal line test for question 3a part 1 to prove that f has an inverse?
you can! lol cos i lazy draw graph. so pls the horizontal line test works fine!
How bout question 12? If I state X1 + … X5~ N ( , ) but I didn’t explicitly show my calculations. Will any marks be deducted? Thanks for taking answering our doubts! Really appreciate ur effort! Do have a nice day 🙂
means you never show like at least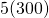 those? haha might lose a mark or two for each part, since they did write explicitly for you to state any distribution you use explicitly. :/ Furthermore, the questions aren’t that hard honestly (no tricks too) and the “lines” you can read are probably the part whereby you find the parameters of the distribution.
those? haha might lose a mark or two for each part, since they did write explicitly for you to state any distribution you use explicitly. :/ Furthermore, the questions aren’t that hard honestly (no tricks too) and the “lines” you can read are probably the part whereby you find the parameters of the distribution.
Pleasure, all the best for you remaining papers!
Omg! Which means I’ll deduct 4-5 marks?
cos if you think about it, the parts all quite easy ah. :/ i think must show the bare minimum calculations la, even if you dont put like E and Var.
Hello! I also did what you did, like I stated all the distributions I used like X~N(mean,variance) without showing calculations. I think if you got the final answer right then you shouldn’t minus any marks? Because that’s what I do for all my internal exams and what my school tutor from RJ encourages us to do if we can to safe time :/
Apparently if it says state explicitly, just state can already… unless Mr Teng can confirm otherwise?
Thanks!
Hi Mr Teng, thank you for the reply earlier! I just realised that I didn’t state parameters clearly for question 12, how many marks will that deduct? And also, for the continuity correction, I didn’t write (by c.c) how many marks will that deduct too? 🙁 Thanks in advance!
Hi I scored about 155/200 possible to get A? :((((((
I really worked hard on math and my careless mistakes cost me quite a lot of marks and being optimistic I think I’ll get 150/200 is it enough for an A?
optimistically, yes. 🙂 I think you’re just on the dot. its either a high B or a low A that sorts if you get what i’m saying.
if i got the p-value wrong but everything right for the hypo testing, how many marks would be deducted?
And for the last qn last part, i got the variance wrong because i typed in the calculator wrongly but everything else even though my final answer is wrong, how many marks would i get?
Thanks!!
Hi, will i lose all the marks for 6ii and 6iii if my continuity correction is wrong? I wrote 30.5 instead of 29.5 🙁
Hi there!!!
82/100 for paper 1 and 76/100 for paper 2! What are my chances?? Is it possible for an A considering how so many ppl consider it easy ( I find it manageable, not very easy coz there are too much room for careless mistakes)
Thanks in advance
i think this paper really test students on precision. So thats something, everyone will struggle with, now and then. I know a lot find it manageable and easy too. most of them minus marks for the careless mistakes.
As for your grade, I think thats fine, you should be able to get A if all is well, like just nice ba 🙂 Don’t worry. All the best for the other papers!
Dont kmow why but i couldnt do the first question lol. I finally did it in the laat 30mins but i didnt integrate it normally. I used substitution method. I still ot the answer so it should be fine right? I think too hard and didnt see that it could be integrated easily.
it happens. I can’t do p6 models anymore eh. :/
I really worked hard on math and my careless mistakes cost me quite a lot of marks and being optimistic I think I’ll get 150/200 is it enough for an A?
i’m honestly really worried hahah everyone (literally everyone) here seems to be getting 70… 75.. . truthfully, i did okay for paper 2 but i flunked paper 1, is the national average really 70/75 lol. to be honest, i’m from a top tier jc though by no means do i consider myself to be smart of mathematically-inclined. if everyone from a lower tier jc obtains >80 (i read a comment somewhere), while people in my school are looking at 60+ – 70+, i’m worrying a lot here.
I think there are a handful of troll comments (especially the >80), which I didn’t really go down the list and remove all, only some. Statistics don’t lie, well at least, thats my belief, considering I deal with statistics almost daily, so you dont exactly need to worry that much. And whats your definition of flunk haha.
I think most of them got marks around 70-75, probably, and to get A, you will want to squeeze into the median. But that shouldn’t be like national mean mark, a bit too high. Pls dont worry and look forward to your next papers.
my definition of flunk is really bad, i shan’t sugarcoat it, i got an E. Even i know that i’m not close to the 50th percentile, i know an A is not even in my reach but i’m hoping for a B.. my second paper is a lot better, possibly a high b and a low a. but even a b looks hard to get now. thank you so much for the assurance though 🙂
I see. Don’t worry so much since the paper is over. You should focus on papers that are still within your control. One of my j2 just threw the exam paper away after the exam haha.
All the best for the rest of your papers 🙂
Hi, if I get 157/200 is that an A or B??? I’m really worried
should be A la. dont worry. 🙂 Cos it seems like there is a gathering around 70-75, breaking that barrier should put you around median. Dont worry. more papers coming. All the best!
Thank you!!!! So much
pleasure. all the best 🙂
Hi I would like to ask
For hypo testing question, if I used z-test instead of t-test but got the estimates correct, how many marks can I get? 🙁
for the hypo testing if i didn’t use left tailed test but used 2 tailed test but coincidentally the conclusion is correct, where we ‘do not reject’ but my p value is twice that of the answer, how many marks will i get?
The unbiased estimates are correct too.
You should get 2 marks for the estimates since they want you to find it. So you used T-test, then it should be 1-2 marks for the method.
Hi I would like to ask
For the hypo testing question, if I used z-test instead of t-test but got the estimates correct, how many marks can I get? 🙁
Hi, was wondering if for q7(i), would it be accepted if i wrote number of errors per line instead of number of errors per page? Haha. Bcos before the exam i heard that it should be something like a subset of what the qns asks but i think i misunderstood this?
should be per page. you’re actually change the “space” here. its based on the definition given haha
Hi Mr Teng , I have some questions regarding the paper . 1. For the correlation and regression qn, if I calculate all my r value wrongly, can I still get 1 or 2 marks for the subsequent parts ? 2. For the function qn , shouldn’t 1-rt3/2 be excluded since it is the asymptote ? 3. For the PnC qn , last part , I Found the two cases and took 10080-5040 but forgot to add 720. Will I still get some marks. Thanks !
i think you should get the marks for correlation since the bundle the marks as 3, i will believe that its based on how many you’re correct. there should be method marks subsequently.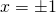 and
and 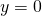 . think you got it mixed up.
. think you got it mixed up.
why excluded? thats actually the turning point, the asymptotes are
yes you should be awarded your rightful method marks still.
Hi Mr Teng, if I get 0.165 correct for the min P (A’nB’nC’) but not for the max 0.33, can I get half the marks?
yup, i would think you get half the marks.
Hi Mr Teng, I am from AJC and I got 160 total , excluding the marking marks. However, i spoke to my friends and most of them got around 170 and above, it appears to be the same case for my other friends from RJC and HCI….. Do you think i can still get my A, considering that the friends i spoke to all said the paper was super easy and all of them got 170 and above???
yes, thats what i gather from my students from these schools too haha. and dont discount njc, nyjc & acjc. but I guess, there will be a portion struggling too. I would think 160 is good for A, 170 is like confirmed A haha. I dont know what is the sufficient mark though. :/ haha
yeah you’re right, the 30% from RJC and HCI are claiming that they got around ~70 for both papers here
Hi can I check for 9ii (probability)? They say “given also that B and C are independent”, which added on to the initial info means AB, AC and BC are 3 pairs of independent events. Is there anything wrong if I do P(A’) * P(B’) * P(C’) to get P(A’ n B’ n C’)? The answer I get is 0.231 (from 0.55 * 0.6 * 0.7)
Is it ok to predict one grade up from our school grading like 50+ is a D so it may be a C at A levels and 60+ is a B so it may still result in a B at A levels? ( since it’s unreasonable to expect A for 60s range judging from the performance)
something like that la. but must school also. different school, different standards of people and cohort, different statistics. and A-levels is the time whereby all gather together and its quite hard to extrapolate from a single sample of school haha
is it really possible for 50% of the cohort to get >75% overall? Considering most will have a fair portion of careless mistakes as well as conceptual errors, isn’t it quite difficult for 50% of singaporeans to get that high?
I’m from a top tier JC and on average people are losing about 20 or so marks per paper, but then again my sample size is quite small and theres a likelihood that it is not very accurate. That said wouldn’t students from the lower tier JCs struggle to hit this 70++%?
yea, why not. just score >150/200 based on 75 marks, thats 50 marks to minus off, which will satisfy the average 20 marks per paper. you’re quite right to say 50% of the JC2, but thats just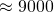 and some schools do have above national average distinction, some kind of spillage problem haha. I’ll say that statistically, more students from the lower tier JCs will struggle then, similarly more students from top tier JC will struggle lesser. purely from the numbers la haha
and some schools do have above national average distinction, some kind of spillage problem haha. I’ll say that statistically, more students from the lower tier JCs will struggle then, similarly more students from top tier JC will struggle lesser. purely from the numbers la haha
yeah i guess you are right about that. Considering RJ/HCI have >70% and VJ alone has around 65-70%, that totals to about 2000 or so students already. So about 7000 As to go around for the remaining JCs which includes AC NJ and whatnot. I’m getting about 140-145 /200 and tbh I think I can’t get the A already. Anyway thanks for the solutions and replies to the comments 🙂
haha, dont keep thinking of the upper half. Should always remember there is a lower half too. 🙂 Dont worry so much. and all the best for your remaining papers!
Can I get a C with 57 marks overall based on the bellcurve ?
Probably, if we are optimistic. 🙂
range for c grade ?
Hi Mr Teng, I know a lot people been asking you the same few questions but I would really like to get some reassurance!! I estimated my marks to be 140/200 (I didnt take into account method marks at all, once i saw that my answer was wrong i take it as the whole part wrong). Is there a chance for me to get A? :/ Im from one of the so called good jc at bukit timah but P1 seems to be bad for my schoolmates
a few of my students did similar style as you haha. i think shouldn’t be too much of problem then, cos there will be method marks one, so should push to bout 150+ one. 🙂 And must define bad though, dont be too harsh on yourself. all the best for you remaining papers!
Hi Mr Teng, for q12, if i never show the workings like Var(x)=5(300)=1500,
but jus write Var(x)=1500,
will i get penalize? i got wrote E(x) and Var(x) for all distributions.
thx in advance
I think it should be okay, provided you define the variables well though.
Hi, for question 12 one of the last parts, may I ask why did you minus your variance for 5 apples and 8 pears? Isn’t variance of normal dist only allowed to be added ö
oh right. my bad. typo, the calculation still correct. thanks for pointing it out.
Hi Mr Teng,
What’s a safe mark for B!
Thanks for posting this as well! 🙂
Hi Mr Teng,
What’s a safe mark for B!
Thanks for posting this as well! 🙂
Q scared but I’ll be satisfied with a B!
Hi! I couldnt prove the MI question at Pk+1. I have no idea why but I rmb getting something similar to your answer. How is the 6marks allocated for that MI question?
i think you either need to be able to factorise your working to prove, or expand the p(k+1) statement to prove. You perhaps didn’t do one of them. The proving part should be 3-4 marks.
Hi sir. I realised after the paper I made alot of careless mistakes and yeah I lost a whole lot of marks. Im standing at about between 115-122/200. I doubt a B is possible. How about C?
Probably a C but if you’re lucky, you might hit a low B. Let’s hope for the best 🙂
Alright sir. Thanks alot
For question 4(b)(3) if my value of n is wrong. But I did correctly show what the sum to infinity is,will I still get 1 mark for showing the sum to infinity?
You should. Since the working is quite short too
Hi Mr Teng for question 4 (b) part 3 my value of n is wrong but I did correctly calculate and show the sum to infinity. In this case will I still get 1 mark for showing the sum to infinity?
yes, you should.
Mr Teng, if the hypothesis testing question I used Z-test, but I got the unbiased est. of the mean and variance correct + the hypothesis correct (left tailed test) i would have gotten the same conclusion. Do i -3 or -4 marks though (the question is 7 marks). By the way, do you think 155-158 marks is safe for an A! Thank you for taking your time to read this post!
i think that mark is okay for an A. 🙂 The estimates should give 2 marks themselves since they did ask you to find. The wrong test might cause you 2-3 marks if thats your only error.
Alright 🙂 my paper 2 mark was lower than my paper 1 mark surprisingly (super careless haha :P) but thanks again for your reply!
pleasure. all the best for your remaining papers 🙂
Is 152 safe enuf for an A? Provided that i didnt minus off some method mark that i am unsure whether i will get?
you will get A as long as you get >120
Are you the same troll as the one who said need 170 to get A?
Mr Teng for the mathematical induction question if during the last part where I’m supposed to prove that p(k+1) is true. I did not state ‘based on the assumption that p(k) is true’ when showing how summation of the first k terms is converted to another term. Will I lose marks for that? I did show the assuming p(k) is true part earlier and I managed to prove the statement true too.
Hi Mr Teng for the mathematical induction question I did not state ‘ based on the assumption that p(k) is true when I converted summation of the first k terms to another term ‘.will I lose marks for that?I did state earlier the assume p(k) is true part and also I managed to prove the overall statement correctly.
Hi Mr Teng, how many marks wil I lose if I prove p(k+1) using Ex^3=n^2/4(1+n)^2 , Ex^2=n/6 (2n+1)(n+1) formulas instead?
Hello if I didn’t write the conclusion for the hypothesis testing properly how much mark will be minus! Thank you !
haha how wrong is the conclusion? tbh, i think so long as you mention that you do not reject and there is insufficient evidence then okay alr.
If i got around 75 for paper 1
and 72 for paper 2 WILL MY A BE SECURED??? PLEASE MY MUM WILL SCOLD ME IF I DONT GET A
haha, i really can’t say whats secure, thats like saying sufficient mark. hmm just be optimistic and focus on the other papers. all the best!
For MI is it ok if I start from n=0, if not how many marks deducted?:( also I used a z test will I lose all my marks:( Thanks for your help!
you can’t start from n=0 since the question starts with n=1. but theoretically, MI is still fully functional and logical and will still allow us to prove P(n) soundly. so it really depends on how they want to mark you. might get the full 6m, or minus one. :/
I’m not sure if my comment got posted – anyway is it ok if for MI started from n=0? And for hypo testing I used z test instead will I lose all the marks :/ thank you
you will probably lose like 3 for the wrong test, given that you found the correct unbiased estimates and had the correct hypotheses too.
Hi, under what circumstances are method marks awarded? For example if the correct formula is used but wrong values substituted in as a result of careless, is method mark awarded?
its awarded based on correct methods lo haha. but wrong values will result in loss of answer mark.
hi sir. for qns12 last part, how many marks do u think i can get if i got my mean right, variance wrong but method correct? thank you for taking ur time to ans our questions 🙂
wrong method, as in the inequality wrong? or the distribution haha. 2-3, depending on your answer.
erm inequality was right but i calculated the variance wrongly so my final ans was wrong 🙁
Hi, is it wrong if I use I got n> or equals 499? and for the disadvantage of quota sampling could I say it’s biased cause friendlier oeoole will be more likely to respond? Thank you
hmm, the bias arise from the surveyor, not the respondents. :/
thats fine, so long as you conclude n = 499
Hi may I ask if am I able to secure a B with 130/200? (assuming any fo my wrong answers to be counted as a zero)
should be possible. Don’t worry.
Well, to be fair, the pure maths section for Paper 2 this year is definitely more “manageable” than the past 2 years. The statistics side are ok except for the probability qn with 3 sets which I have never encountered before as it is the normal 2 sets. The PnC this year is definitely more ok than the 2013 paper. So for a rough gauge of As.. My logic will be between the minimum A for 2013 and minimum A for 2014. P.S. The percentage A rate is quite high on national level. So long Cambridge don’t see fundamental presentation and Algebraic errors, It shouldn’t be a big problem to score an A. 😀
Is 77% enough for an A?
possibly Don’t. worry. 🙂
Can I get A with paper 1 87 and paper 2 67? 🙁
still possible. 🙂 Don’t worry!
Is 87 for paper 1 and 67 for paper 2 sufficient for an A? 🙁
What if for null hypothesis H0 i put it as M> or= 90? And the rest are all correct. Will it make alot of difference? Since the qn said that the minimum mean is 90?
And for q4biii, is there another possible way of interpreting the qn? The qn was within 10^-3 of the sum of infinity i didnt interpret it as +/- 10^-3 of sum of infinity but rather within 1/10^-3 of sum of infinity. So i got 1499
you will probably lose the mark for the hypothesis. the test for which the null involves an inequality is quite different, and isn’t taught in A-levels actually. 😕
Wld i lose alot of marks? Or wld i get some method marks?
Hi sir, just want to ask for paper 1 Q4 if they will award any marks at all if I differentiate with respect to the wrong term? Even though d is a fixed value I was rushing for time and I used dA/dd. But stating the total area should guarantee at least a mark right?
And if you are the examiner and I accidentally provided double answers for the volume of revolution (i.e qn 10iii) would you ignore the whole question or give marks for workings? I forgot to strike out one of my answers
you should get marks for the equations, but you will be mistaken for differentiating wrt to d.
if i practice positive marking, you might get the marks. after all, you dont minus marks for Alevels, you only dont earn the method marks.
Hi sir, just want to ask for paper 1 Q4 if they will award any marks at all if I differentiate with respect to the wrong term? Even though d is a fixed value I was rushing for time and I used dA/dd. But stating the total area should guarantee at least a mark right?
And also, if I accidentally provided double answers for the volume of revolution (i.e qn 10iii) would you ignore the whole question or give marks for workings? I forgot to strike out one of my answers
117/200. Can get C or B?
Just one question. 116 marks. B or C? Just asking
not B nor C, its an A for sure
for qn 7(iii), I failed to write an equation in terms of n but solved using my GC and demonstrating proper working, will i still be able to clinch 1out of 2 marks given that I got the correct answer?
yup definitely. if not for that “show” statement, then you should get full credit.