Understanding A-level differentiation questions

Many students seem to know how to solve a Min/ Max problem easily but do not understand. I hope this gives them some insights into Min/ Max problem.

Firstly, what is a Min/ Max problem? It is those differentiation questions that ask us for the largest area, smallest volume, minimum cost, etc. All of this falls under a simple idea of minimum or maximum problem.

Credits: A-level H2 Mathematics (9740) Paper 1 2010 Question 9

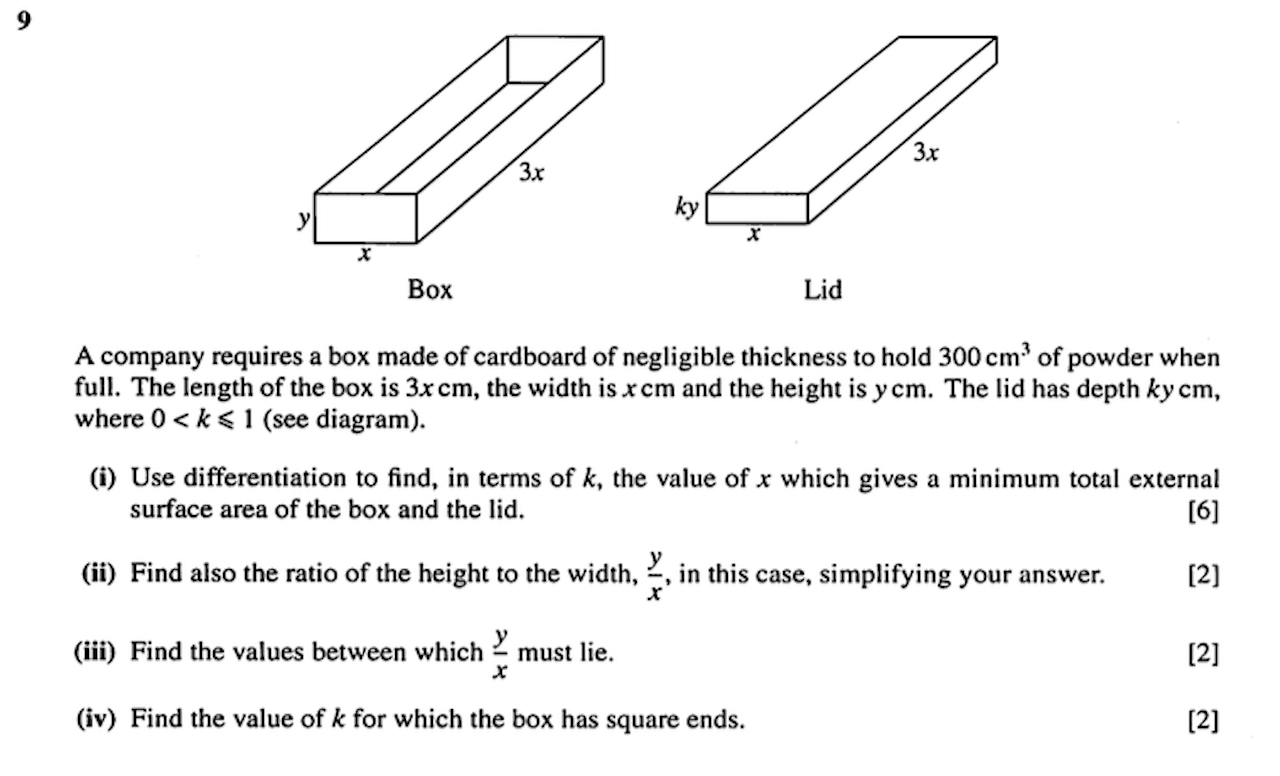
Take the above question as an example. Here, we are trying to obtain the minimum external surface area. So most students should be able to say they will find an equation of area and then differentiate it, equate to zero and solve.

So how does this relate in real life?

Most products you see in supermarkets, are related to such a problem. We have a constraint usually, in this case volume. And we have factors we can vary, in this case, the dimensions which affects the surface area. We want to minimise it simply to cut costs. Other words, given this single constraint of volume, we find the dimensions of the box that gives the smallest surface area.

The equation of area we found is a graph and when we equate the first order derivative to zero, we are attempting to find stationary points which can be either maximum or minimum points here, that is, the minimum area or maximum area. Then we check with the second order derivative to show it is indeed a minimum area.

Some students do ask, but in reality, we would’ve more constraints like weight, etc. To learn more on this, you can read more on lagrangian function which allows us to consider even more constraints. This will require knowledge beyond A-levels.

Solutions to this questions can be found here.