2013 A-level H2 Mathematics (9740) Paper 2 Question 4 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
cos{\theta}=\frac{|\begin{pmatrix}2\\-2\\1\end{pmatrix}{\bullet}\begin{pmatrix}-6\\3\\2\end{pmatrix}|}{\sqrt{9} \sqrt{49}}=\frac{16}{21}

\theta = {40.4}^{\circ}

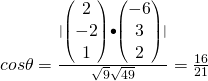
(ii) Using Graphing Calculator, equation of line,

r = \begin{pmatrix}{-\frac{1}{6}}\\{-\frac{2}{3}}\\0\end{pmatrix} + \lambda \begin{pmatrix}7\\10\\6\end{pmatrix}, \lambda \in \mathbb{R}

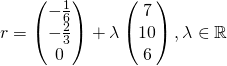
(iii)
Distance A to 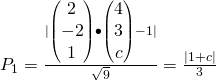P_1 = \frac{|\begin{pmatrix}2\\-2\\1\end{pmatrix}{\bullet}\begin{pmatrix}4\\3\\c\end{pmatrix} - 1|}{\sqrt{9}} = \frac{|1+c|}{3}

Distance A to 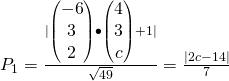P_1 = \frac{|\begin{pmatrix}-6\\3\\2\end{pmatrix}{\bullet}\begin{pmatrix}4\\3\\c\end{pmatrix} + 1|}{\sqrt{49}} = \frac{|2c-14|}{7}

\frac{|1+c|}{3} = \frac{|2c-14|}{7}
49(1+c)^{2} = 9(2c-14)^{2}
c = -49 \mathrm{~or~} \frac{35}{13}

KS Comments:

Some students have slight confusion about how to evaluate the modulus, mainly cos they confuse over are the applying modulus to a scalar or vector quantity.

Comments
    pingbacks / trackbacks
    • Thoughts of H2 Math 2015 | The Culture

      […] paper has some questions that springs a surprise and throws students off their feet. In 2013, we saw the distance with two planes. In 2011, we saw a trigonometry Mathematical Induction. In […]

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt

    Start typing and press Enter to search

    2013 A-level H2 Mathematics (9740) Paper 2 Question 3 Suggested SolutionsJC Mathematics
    2013 A-level H2 Mathematics (9740) Paper 2 Question 5 Suggested SolutionsJC Mathematics