All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
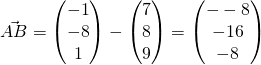
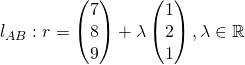
(ii)
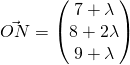 for some
for some ![]() .
.
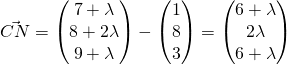
Since ![]() is perpendicular to
is perpendicular to ![]()
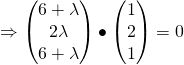
![]()
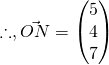
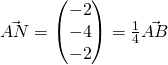
![]()
(iii)
Let C’ be the point of reflection of C in line AB.
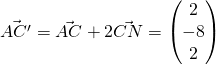
![]()
KS Comments:
A few steps above are being skipped as it is really inconvenient to type the vectors in LaTeX. Please let me know if it caused problems for you.
