All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
Let ![]()
![]()
![]()
![]()
![]() , since
, since ![]() for all domain of
for all domain of ![]() in g, g is self inverse.
in g, g is self inverse.
(ii)
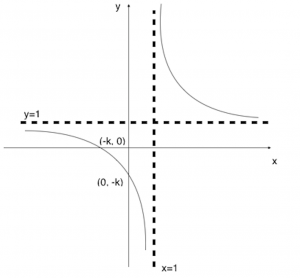
(iii)
Line of symmetry is y = x.
Required transformations are as follow, in order.
1. Translate the graph by 1 unit in the positive x-axis
2. Scale the graph by factor (k+1) units parallel to the y-axis
3. Translate the graph by 1 unit in the direction of the positive y-axis
KS Comments:
The term “self-inverse” made some students confused as they were unsure what it means. It means that g is its own inverse. The easiest way to draw this curve is to first identify the asymptotes, then substitute x = 0 and y = 0 to resolve for the axial intercepts. For (iii), students must learn to describe fully, using the correct key words and terms.