Many students have asked me about Mathematical Induction, like whats the idea behind it. Especially since I always emphasize the importance of 
.
So lets try to make some sense of this long and mundane proof.
Our first step always seek to prove that is true. And then 
is our induction hypothesis, think of it as an assumption (so it might or might not be true). We then seek to prove 
is true with the use of . Should we succeed in proving it, we establish some relationship between and . But if we trace back, was a mere assumption. So where do we go from here?
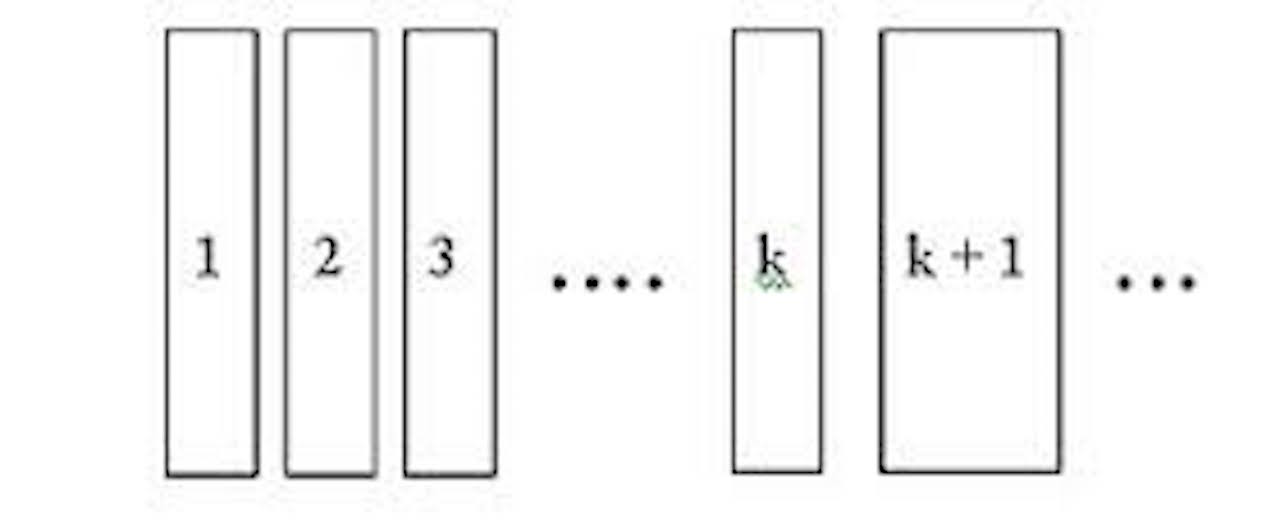
Credits: www.open.edu
If we trace back to , then we will create a domino effect like the above. Since we have that is true definitely, using the proven relationship with and , we can establish 
is true. Here, we create a huge domino effect up to n.
Inquisitive students have asked me before, what if k is greater than n? Now that’s a much profound question to be answered. But curious students can google “Strong Mathematical Induction”.
