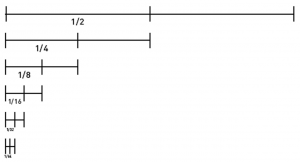
If KS travels half the distance to the bus stop for every move, will he ever reach the bus stop?
The answer is that I will never reach the bus stop, but could make arbitrarily close to it. This excellent example of an geometric progression is called the dichotomy paradox.
We all know that to prove that a GP converges, show ![]() . But I’ve heard a handful of students asking why. So today, lets break it down together.
. But I’ve heard a handful of students asking why. So today, lets break it down together.
The very idea of |r|
If ![]() , it’s obvious that my GP converges.
, it’s obvious that my GP converges.
If ![]() or
or ![]() , we can suggest that r is simply a decimal number less than +/-1, then r^n will simply get smaller as n increases, until it is arbitrarily so small that it’s almost 0. Even if we say r = 0.99999, 0.99999^1000 will not give you 1, it instead, gives you a really small number.
, we can suggest that r is simply a decimal number less than +/-1, then r^n will simply get smaller as n increases, until it is arbitrarily so small that it’s almost 0. Even if we say r = 0.99999, 0.99999^1000 will not give you 1, it instead, gives you a really small number.
I hope these helps to clear the air for this condition. A food for thought, if I am not given the value of r, will I still be able to prove if it converges? 🙂

[…] Will it ever converge? 2. Intuition of Mathematical Induction 3. Things you might want to know when making a […]