We shall look at an easy method of remembering or knowing how to derive the sum to product formula. As you see below is the product to sum formula:
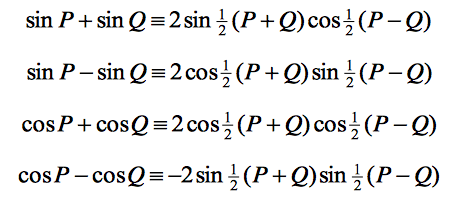
Credits: SEAB
We first let
![]()
![]() , and thus have,
, and thus have,
![]()
![]()
The first formula should look like this:
![]()
is being taken care of too but be careful that there is a “2” there.
This little switcheroo will allow us to be at the doorsteps of the sum to product formula. Students should attempt the substitution yourself, and you will realise that it is not that hard after all. This should ease your life of finding P’s and Q’s. Try deriving the remaining three formulas!
Please comment at the bottom if you run into any questions, I will love to help! 🙂

[…] and think of using method of differences. The MI requires students to know how to find the product to sum and sum to product formulas using the MF15, which many students do not realise how to […]
[…] Substitute into given differential equation, Since Using the product to sum formula as shown here, we […]
[…] How to derive the sum to produce formula 2. Integrating Trigonometric Functions (1) 3. Integrating Trigonometric Functions (2) 4. […]
[…] some of their uses in A’levels. I’ve previously discussed the use of factor formulae here under […]