This page contains all questions and answers asked by students from this class. The most recent questions will be at the top.
Differentiate
Substitute
Since
Using the product to sum formula as shown here, we have
Note:
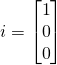 and
and 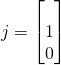
Using GC,
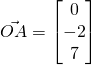
![]() — (1)
— (1)
![]() — (2)
— (2)
![]() — (3)
— (3)
Using GC, 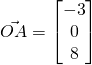
Qn11
(i)
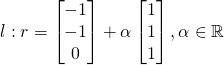
(ii) Since l is the common line of intersection on
1. l must be parallel to
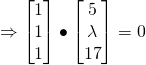
2. Given that l is parallel to
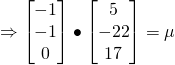
(iii)
For 3 planes to have nothing in common, then l must be parallel to
But
12.
(i)
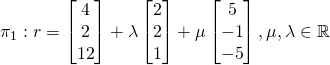
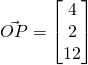 is on
is on 


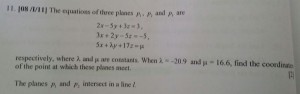

[…] Sun 930am H2 Math Sun 1130am H2 Math Sun 2pm H2 Math Mon 2pm H2 Math Mon 430pm H2 Math Mon 730pm H2 Math Tue 5pm H2 Math Tue 7pm H2 Math Thur […]