2014 A-level H2 Mathematics (9740) Paper 2 Question 4 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(a)
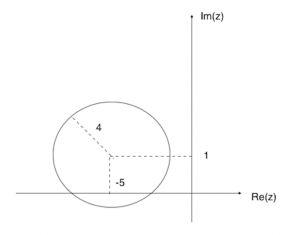
(i) Locus of z is a circle with centre (-5, 1) and radius 4.

Graph for 4(ai)

Graph for 4(ai)

(ii)
By Pythagoras’ Theorem, x^{2} + x^{2} = 16 = 2 \sqrt{2}
z = -5 + 2 \sqrt{2} + i(1 - 2 \sqrt{2}), z = -5 - 2 \sqrt{2} + i(1 + 2 \sqrt{2})

(b)
(i) |w| = 2, arg(w) = -\frac{\pi}{6} \Rightarrow w = 2 e^{-i \frac{\pi}{6}}
w^{6} = (2 e^{-i \frac{\pi}{6}})^{6} = 64 e^{-i\pi} =64 e^{i\pi}

(ii) \frac{w^{n}}{w^{\ast}} = \frac{(2 e^{-i \frac{\pi}{6} } )^{n}}{2 e^{i \frac{\pi}{6}}} = 2^{n-1} e^{- \frac{i(n+1) \pi}{6}}

arg(\frac{w^{n}}{w^{\ast}}) = - \frac{i(n+1) \pi}{6}

For \frac{w^{n}}{w^{\ast}} to be real, - \frac{i(n+1) \pi}{6} = -\pi, -2\pi, -3\pi, ...

\therefore, \mathrm{smallest} \thinspace n = 5, 11, 17

Personal Comments:
Students should use a compass and projector to draw the locus in (ai). The locus in (aii) is not required to be drawn, should students want to draw, I suggest they draw a new figure for it and not construct on that of (ai). Students that struggle to be neat, can always use the graph paper provided, but please do label the question properly. For (bi), some students forgot that 0 \le \theta \textless 2 \pi was stated by question and did not change it.

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    2014 A-level H2 Mathematics (9740) Paper 2 Question 3 Suggested SolutionsJC Mathematics
    2014 A-level H2 Mathematics (9740) Paper 2 Question 5 Suggested SolutionsJC Mathematics