2013 A-level H2 Mathematics (9740) Paper 1 Question 5 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)

Graph of 5i

Graph of 5i

(ii)
Since x=asin\theta, we have dx=acos\theta ~d\theta
When x= \frac{\sqrt{3}a}{2}, \theta = \frac{\pi}{3}
When x= \frac{a}{2}, \theta = \frac{\pi}{6}

\int_{\pi / 6}^{\pi / 3} \sqrt{1-sin^{2}\theta}~(acos\theta) ~d\theta

= a \int_{\pi / 6}^{\pi / 3} cos^{2} \theta ~d \theta

= a \int_{\pi / 6}^{\pi / 3} \frac{1+cos2\theta}{2} ~d \theta

= \frac{a}{2}[\theta + \frac{sin 2 \theta}{2}]\biggl|_{\pi / 6}^{\pi / 3}

= \frac{a \pi}{12}

KS Comments:

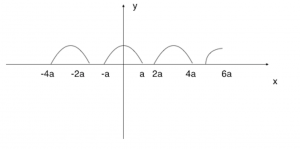
The function is a periodic curve and some students do have problem reading such functions. They should be alert of the domain that they are required to draw too. Some students were unsure how the hint that f(x+3a)=f(x) should help. The parametric integration should be quite simple to handle as students just need to be cautious and introduce the double angle formula from MF15 effectively.

Showing 3 comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    2013 A-level H2 Mathematics (9740) Paper 1 Question 4 Suggested SolutionsJC Mathematics
    2013 A-level H2 Mathematics (9740) Paper 1 Question 6 Suggested SolutionsJC Mathematics