All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
Numerical Answers (click the questions for workings/explanation)
Question 1: ![]()
Question 2: ![]() , other roots
, other roots ![]() ,
, ![]()
Question 3: ![]()
Question 4: ![]()
Question 5: ![]()
Question 6: ![]()
Question 7: ![]()
Question 8: ![]()
Question 9: ![]()
Question 10: ![]()
![]()
Sub ![]() .
.
![]()
![]()
![]()
(ii)
![]()
![]()
Required coordinates: ![]()
![]()
Comparing the coefficient of ![]() ,
, ![]()
Comparing the coefficient of ![]() ,
, ![]()
Comparing the coefficient of constant, ![]()
Comparing the coefficient of ![]() ,
, ![]()
![]()
![]()
![]()
![]()
Other roots are ![]() .
.
(bi)
![]()
![]()
![]()
![]()
![]()
Other ![]()
(bii)
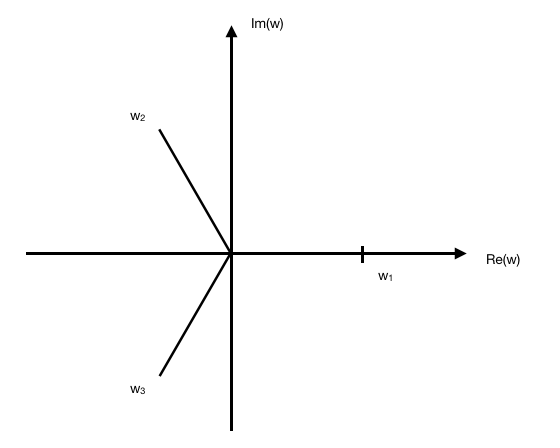
Using GC,
![]()
![]()
![]()
Note: they should be drawn at equal lengths of 3 units and 120 degrees apart from each other.
(biii)
![]()
![]()
They are the coefficients of ![]() actually.
actually.
Since ABCD is a parallelogram,
![]()
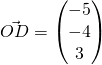
![]()
(ii)
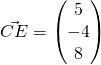
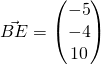
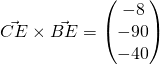
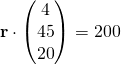
![]()
(iii)
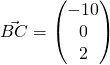
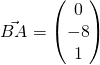
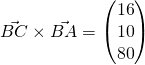
Required angle 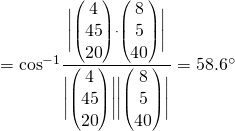 (1 DP)
(1 DP)
(iv)
Midpoint 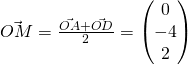
Distance of ![]() to plane is equals to the length of projection of
to plane is equals to the length of projection of ![]() onto the normal.
onto the normal.
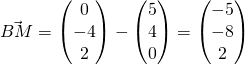
Distance required 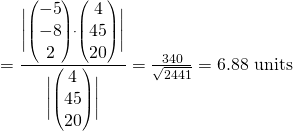
![]()
![]()
![]()
![]()
![]() for the expansion to be valid since
for the expansion to be valid since ![]() , thus
, thus ![]() is not in the domain.
is not in the domain.
(ii)
![]()
![]()
![]()
![]()
![]()
![]() (4 DP)
(4 DP)
(iii)
Using GC, ![]() (4 DP)
(4 DP)
A sample size of 30 will be sufficiently large for the manager to approximate the sample mean distribution to a normal distribution by Central Limit Theorem.
The fans should be randomly chosen, i.e., the probability of a fan being chosen should be equal and the fans are chosen independently of each other.
(ii)
Let ![]() denote the time to failure, in hours
denote the time to failure, in hours
Let ![]() denote the population mean time to failure, in hours.
denote the population mean time to failure, in hours.
Let ![]() denote the null hypothesis.
denote the null hypothesis.
Let ![]() denote the alternative hypothesis.
denote the alternative hypothesis.
![]()
![]()
(iii)
Let ![]() be the required variance.
be the required variance.
Under ![]() ,
, ![]() approximately by Central Limit Theorem since the sample size is sufficiently large.
approximately by Central Limit Theorem since the sample size is sufficiently large.
To not reject ![]() at 5% level of significance,
at 5% level of significance,
![]()
![]()
![]()
![]() (3 SF)
(3 SF)
Let
![]()
![]()
(ii)
For the probability to be greatest, ![]() is the modal value. This means that
is the modal value. This means that ![]() and
and ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(iii)
The probability of not entering the black hole ![]() .
.
Bug take 8 steps regardless of which fork it wants.
Required probability ![]() (exact)
(exact)
Or
Required probability ![]()
Observe that this is a binomial expansion.
Required probability ![]() (exact)
(exact)
![]()
![]()
![]()
![]()
![]()
Thus, events ![]() and
and ![]() are independent events.
are independent events.
(ii)
![]()
![]()
![]()
If ![]() and
and ![]() are mutually exclusive, then
are mutually exclusive, then ![]() .
.
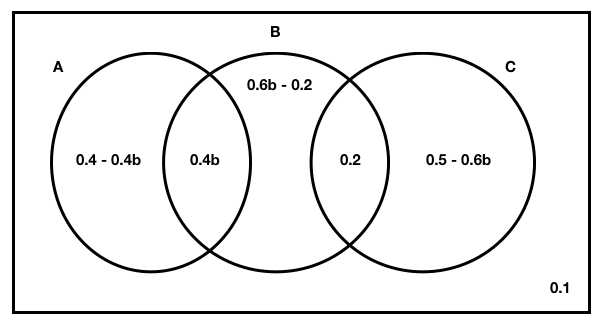
![]()
Note: Students can draw different “designs” so long as you show that A and C does not intersect and they fill up the entire venn diagram.
(iii)
Since ![]() and
and ![]() are independent,
are independent, ![]() ,
, ![]() . We can find the following information.
. We can find the following information.
Suppose ![]() , then
, then ![]()
Suppose ![]() , then
, then ![]()
Minimum ![]()
Maximum ![]()
![]()
![]()
![]()
![]()
![]()
(ii)
When ![]() .
.
In order to have ![]() , two balls numbered 5 needs to be drawn which is not possible since balls are taken without replacement and there is only one ball numbered 5.
, two balls numbered 5 needs to be drawn which is not possible since balls are taken without replacement and there is only one ball numbered 5.
(iii)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
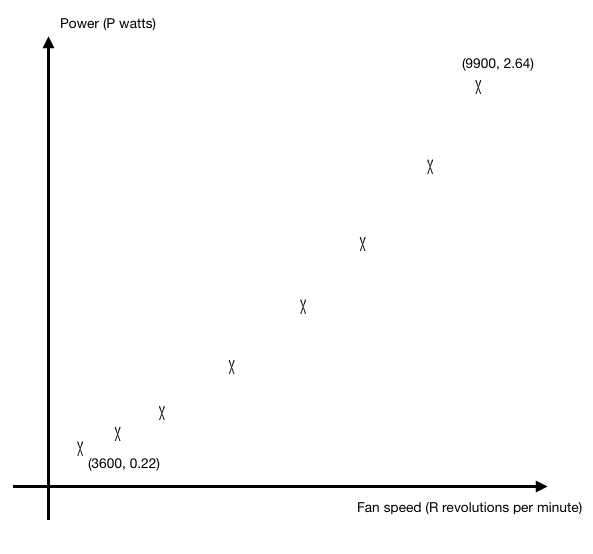
The relationships is unlikely to be well modelled by the equation ![]() . From the scatter, we observe that as
. From the scatter, we observe that as ![]() increases,
increases, ![]() increases at an increasing rate. Thus, a linear model such as
increases at an increasing rate. Thus, a linear model such as ![]() would not be suitable.
would not be suitable.
(ii)
r value for ![]() (3 SF)
(3 SF)
r value for ![]() (3 SF)
(3 SF)
Since the r value for ![]() is close to 1,
is close to 1, ![]() is a better model for the relationship between
is a better model for the relationship between ![]() and
and ![]() .
.
![]()
![]() (3 SF)
(3 SF)
(iii)
![]() revolutions per minute.
revolutions per minute.
Thus estimate is reliable as ![]() is within the given date range and interpolation is a good practice.
is within the given date range and interpolation is a good practice.
(iv)
![]() watts
watts
Thus estimate is not reliable as ![]() is not within the given date range and extrapolation is a bad practice as it assumes the trend continues outside of the data range.
is not within the given date range and extrapolation is a bad practice as it assumes the trend continues outside of the data range.
(v)
Replace ![]() by
by ![]() .
.
![]()
![]() (3 SF)
(3 SF)
(ii)
Let ![]() denote the mass of one type of light bulb, in grams.
denote the mass of one type of light bulb, in grams.
![]()
![]() (3 SF)
(3 SF)
(iii)
Let ![]() denote the mass of of an empty box, in grams.
denote the mass of of an empty box, in grams.
![]()
![]()
![]() (3 SF)
(3 SF)
(iv)
![]()
![]() (3 SF)
(3 SF)
(v)
![]()
![]()
Using GC, ![]() (3 SF)
(3 SF)
(vi)
Let ![]() denote the mass of a randomly chosen box, each containing a bulb and padding in grams.
denote the mass of a randomly chosen box, each containing a bulb and padding in grams.
![]()
![]()
![]() (3 SF)
(3 SF)

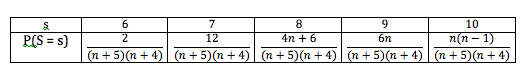


hi i think 9v is wrong as question states R as no of revolutions per minute and as such we must substitute r with r/60 instead please correct me if im wrong