(i)
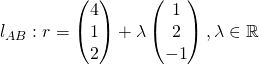
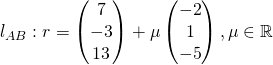
If they intersect, then 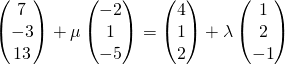 for some
for some ![]()
Solving with GC, we have ![]() . Thus, the lines intersect.
. Thus, the lines intersect.
(ii)
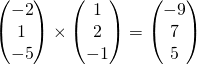
Equation of plane: 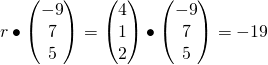
(iii)
Required distance
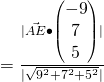
![]()
(iv)
Area of quadrilateral
![]()
![]()
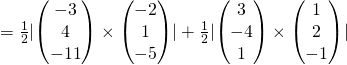
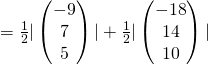
![]()
![]()
(i)
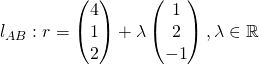
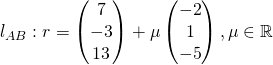
If they intersect, then 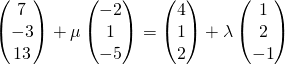 for some
for some ![]()
Solving with GC, we have ![]() . Thus, the lines intersect.
. Thus, the lines intersect.
(ii)
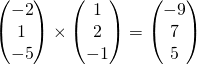
Equation of plane: 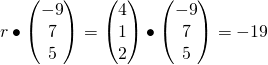
(iii)
Required distance
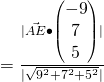
![]()
(iv)
Area of quadrilateral
![]()
![]()
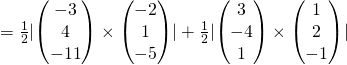
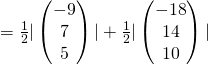
![]()
![]()
[…] June Revision Exercise 8 Q5 – The Culture on June Revision Set 8 […]