We look at the definitions first.
A continuous random variable, X, has a probability density function (PDF), ![]() if
if ![]() and for all events A
and for all events A
![]()
The CDF and PDF are related by ![]()
It is good to know that we have ![]()
We X has a normal distribution, ![]() , and
, and ![]() . And
. And ![]() while
while ![]()
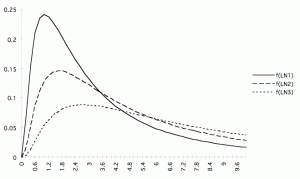
We also have the log-normal distribution, ![]() and
and ![]() . Here,
. Here, ![]() and
and ![]() . The log-normal distribution is very important in financial applications, for starters, the Black Scholes Equation.
. The log-normal distribution is very important in financial applications, for starters, the Black Scholes Equation.

[…] we look at an important concept that is an extension from Bayes Theorem, which we discussed […]