All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
First, translate ![]() 3 units in the positive x-direction.
3 units in the positive x-direction.
Then scale ![]() by a factor of
by a factor of ![]() units parallel to the y-axis.
units parallel to the y-axis.
(ii)
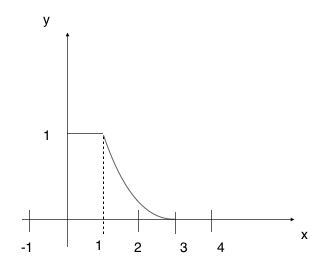
5(ii)
(iii)
Explanation:
![]()
![]()
![]()
Back to 2015 A-level H2 Mathematics (9740) Paper 1 Suggested Solutions
KS Comments:
For the transformations in (i)
There is a lot of different answers thats possible. I just did one, feel free to comment alternative methods.
The graphs here is hard, I did suggest that piecewise function will come out previously but didn’t expect it to be so tricky. The graphs is manageable, but the second graphs is bit more tricky here, as students need to scale out the domain too.

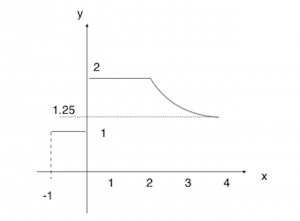

[…] Question 5 Question 5 […]