2011 A-level H2 Mathematics (9740) Paper 2 Question 3 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
Let y = \mathrm{ln} (2x+1) + 3

x = \frac{e^{y-3}-1}{2}

\therefore, f^{-1}(x) = \frac{e^{x-3}-1}{2}, x \in \mathbb{R}

D_f = \mathbb{R}

R_{f^{-1}} = D_f = (-\frac{1}{2}, \infty)

(ii)

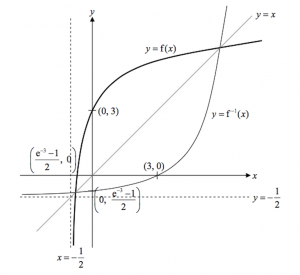
Graph of 3ii

Graph of 3ii

(iii)
f(x) = f^{-1}(x) = x

\Rightarrow f(x) = x

\mathrm{ln}(2x+1) + 3 = x

\mathrm{ln}(2x+1) = x - 3

Using Graphing calculator, x = -0.4847 \mathrm{~or~} 5.482

KS Comments:

Students should be careful to draw the curves according to the given domain. And since the question requests for equations of asymptotes, we should have label them too.

The last part, students can also use the inverse function to solve.

This question, in general did not pose much of a problem for students.

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    2011 A-level H2 Mathematics (9740) Paper 2 Question 2 Suggested SolutionsJC Mathematics
    2011 A-level H2 Mathematics (9740) Suggested SolutionsJC Mathematics