One of the most upsetting things to mark on students’ script is when questions ask them to commend on tangents as ![]() , etc.
, etc.
Following are some example of answers
- ” As
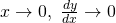 , tangents become flatter and straight.”
, tangents become flatter and straight.” - ” As
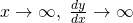 , tangents become straighter and vertical.”
, tangents become straighter and vertical.” - “As
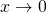 , tangent tends to infinity”
, tangent tends to infinity”
I think a lot of students either have poor understanding of the concepts or don’t think it true. Firstly, tangents is not the gradient so it can’t really tend to infinity. Next, it pains me to read how that explain that tangents become straighter. Occasionally, I’ll ask them to draw me a tangent that isn’t straight after reading such answers.
So a tangent IS a straight line, ![]() . It does not become straighter since it is straight already. So how is a good way to answer such problems and express yourself correctly?
. It does not become straighter since it is straight already. So how is a good way to answer such problems and express yourself correctly?
I tell my students to keep their answers simple, mention the equation if you can find it, or simply explain that tangents are parallel to the y-axis or x-axis.

[…] All tangents are straight lines Prime Numbers and their uses. […]