2011 A-level H2 Mathematics (9740) Paper 1 Question 7 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
\vec{OP} = \frac{1}{3} \underset{\sim}{a}

\vec{OQ} = \frac{3}{5} \underset{\sim}{b}

Using Ratio Theorem in MF15, \vec{OM} = \frac{\vec{OP} +\vec{OQ}}{2}

\vec{OM} = \frac{1}{6} \underset{\sim}{a} + \frac{3}{10} \underset{\sim}{b}

Required Area = \frac{1}{2}|\vec{OP} \times \vec{OM}|

= \frac{1}{2} |\frac{1}{3} \underset{\sim}{a} \times \frac{3}{10} \underset{\sim}{b}|

= \frac{1}{2} |\frac{1}{18} \underset{\sim}{a} \times \underset{\sim}{a} + \frac{1}{10} \underset{\sim}{a} \times \underset{\sim}{b}|

= \frac{1}{2} |0 + \frac{1}{10} \underset{\sim}{a} \times \underset{\sim}{b}|

= \frac{1}{20} |\underset{\sim}{a} \times \underset{\sim}{b}|

(ii)
(a) Since \underset{\sim}{a} is a unit vector, |\underset{\sim}{a}| = 1

\Rightarrow, \sqrt{4p^2 +36p^2 +9p^2} =1

\therefore, p= \frac{1}{7}

(b)
It is the length of projection of \underset{\sim}{b} \mathrm{~onto~} \underset{\sim}{a}

(c)
\underset{\sim}{a} \times \underset{\sim}{b} = \frac{1}{7} \begin{pmatrix}2\\{-6}\\3\end{pmatrix} \times \begin{pmatrix}1\\1\\{-2}\end{pmatrix} = \frac{1}{7}\begin{pmatrix}9\\7\\8\end{pmatrix}

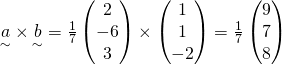
KS Comments:

This question did not pose much of a problem. Most students were able to identify that \underset{\sim}{a} \times \underset{\sim}{a} = 0 comfortably. (iib) however, was not well answered as most students overlooked that \underset{\sim}{a} is the unit vector here thus the projection should be that of b onto a, instead a onto b. Lastly, students should always check their cross product using scalar product like I always advice in class.

Leave a Comment

Contact Us

CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

Not readable? Change text. captcha txt

Start typing and press Enter to search

2013 A-level H2 Mathematics (9740) Paper 2 Question 12 Suggested SolutionsJC Mathematics
2011 A-level H2 Mathematics (9740) Paper 1 Question 11 Suggested SolutionsJC Mathematics