All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
Since ![]() and
and ![]()
![]()
When ![]() ,
, ![]() ,
, ![]()
![]() gradient of C
gradient of C ![]() when
when ![]() .
.
As ![]()
Thus the tangents are parallel to y-axis.
(ii)
(iii)
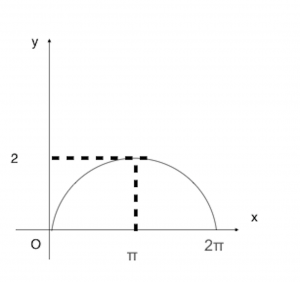
Area ![]()
![]()
![]()
![]()
![]()
(iv)
Normal: ![]()
When ![]()
![]()
![]()
Thus, normal cross x-axis at ![]()
KS Comments:
For (i), some students have difficulties proving. They should note that they found the expression in terms of ![]() but they are trying to prove an expression in terms of
but they are trying to prove an expression in terms of ![]() . This should prompt them to apply the double angle formulas that are found in the MF15. Next, students should learn how to describe the tangents and keep it short and sweet. Some describe tangents become straighter, which is awkward since the tangents are lines. Students can check their definite integral with the graphing calculator.
. This should prompt them to apply the double angle formulas that are found in the MF15. Next, students should learn how to describe the tangents and keep it short and sweet. Some describe tangents become straighter, which is awkward since the tangents are lines. Students can check their definite integral with the graphing calculator.

[…] Question 11 […]