All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
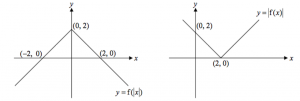
Graph of 5(i)
(ii)

(iii)
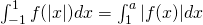
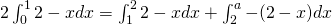
![Rendered by QuickLaTeX.com 2[2x - \frac{x^2}{2}]\bigl|_0^1 = [2x - \frac{x^2}{2}]\bigl|_1^2 + [\frac{x^2}{2} - 2x]\bigl|_2^a](https://theculture.sg/wp-content/ql-cache/quicklatex.com-ee0815bf9b538a62cce9de136457360b_l3.png)
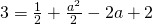
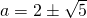
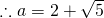 since
since 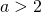
KS Comments:
There are other alternative methods to solving the integration like using the area of trapezoid.
[…] Question 5 […]