2011 A-level H2 Mathematics (9740) Paper 1 Question 10 Suggested Solutions

By KS Teng

All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.

(i)
z^2 = -8i

z^2 = 8e^{i(-\frac{\pi}{2}+2k\pi}

z = 2\sqrt{2}e^{-i\frac{\pi+4k\pi}{4}}

z = 2\sqrt{2}e^{-i\frac{\pi}{4}}, \mathrm{~or~} 2\sqrt{2}e^{i\frac{3\pi}{4}}

z = 2 - 2i, ~ -2+2i

(ii)
Observe we let z = 2w+4, then

(2w+4)^2 = -8i

4w^2 + 16w + 16 + 8i = 0

w^2 + 4w + 4 + 2i = 0

\Rightarrow w = \frac{-4+2-2i}{2}, \mathrm{~or~} \frac{-4-2+2i}{2}

\therefore, w = -1-i, \mathrm{~or~} -3+i

(iii)

Graph for 10(iii)

Graph for 10(iii)

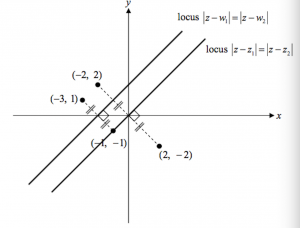
(iv)
Both perpendicular bisector are parallel to each other, so there will be no point of intersections.

KS Comments:

Students should be cautious to leave their answers in cartesian form in (i). For (ii), students can solve by otherwise methods, that is, to use the quadratic formula \frac{-b\pm \sqrt{}{b^2-4ac}}{2a}

Comments
    pingbacks / trackbacks

    Leave a Comment

    Contact Us

    CONTACT US We would love to hear from you. Contact us, or simply hit our personal page for more contact information

    Not readable? Change text. captcha txt
    0

    Start typing and press Enter to search

    2011 A-level H2 Mathematics (9740) Paper 1 Question 6 Suggested SolutionsJC Mathematics
    My Favourite Pure Mathematics TopicJC Mathematics