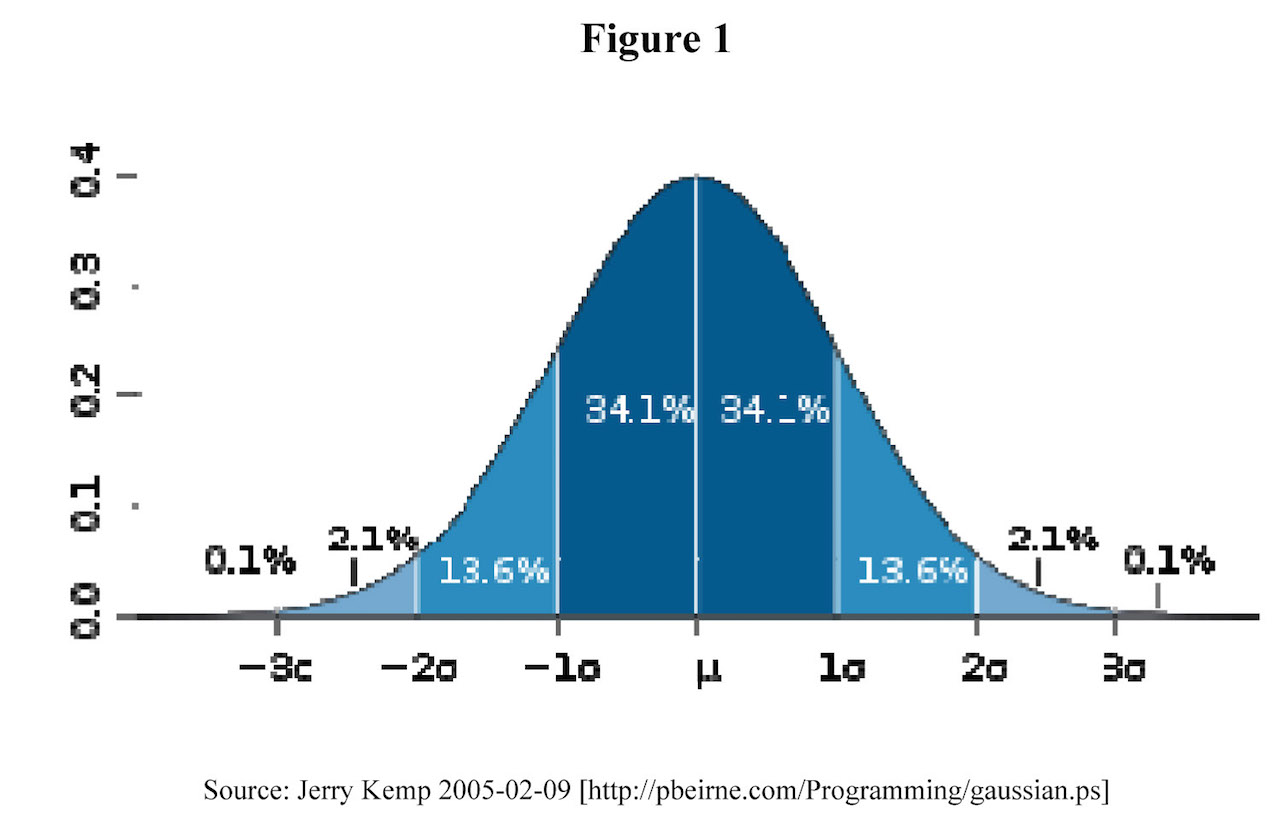
This is a question taken from the 2008 H1 paper. I think it is a simple question that test students on their understanding of what standard deviation mean.
An examination is marked out of 100. It is taken by a large number of candidates. The mean mark, for all candidates is 72.1 and the standard deviation is 15.2. Give a reason why a normal distribution, with this mean and standard deviation, would not give a good approximation to the distribution of the marks.
N.B. We can effectively do Central Limit Theorem here, since n is sufficiently large. So why is it still not a good approximation?
Hint: