All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
(i)
direction of l 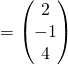
Since planes p and q are perpendicular, the normal of plane p is parallel to plane q.
normal of plane q, n 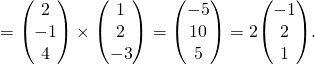
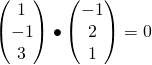
Thus, the cartesian equation of q is ![]() .
.
(ii)
From GC, equation of m is 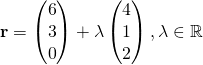 .
.
(iii)
Let 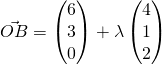 for some
for some ![]()
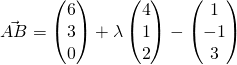
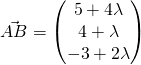
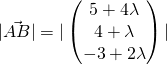
![]()
![]()
![]()
![]()
To find the minimum distance, differentiate ![]() with respect to
with respect to ![]() ,
,
![]()
At minimum distance, ![]() ,
,
![]()
![]()
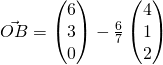
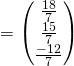
Thus, required coordinates is ![]() .
.
Personal Comments:
The first and second part are standard tutorial questions that students should be able to handle. Students need to realise the use of GC in finding line of intersection is most effective. For (iii), there are several methods, students can complete the square to find the turning point. Alternatively, students can graph the expression found on GC and find the minimum ![]() . They find the same answers too, but it will not be exact. As for students that are keen on following the “otherwise” approach, they can use the foot of perpendicular from A to B on m. Lastly, since the question asked for coordinates, students are expected to give in coordinate form.
. They find the same answers too, but it will not be exact. As for students that are keen on following the “otherwise” approach, they can use the foot of perpendicular from A to B on m. Lastly, since the question asked for coordinates, students are expected to give in coordinate form.
[…] 2014 H2 Mathematics (9740) Paper 1 Question 9 Suggested Solutions […]
[…] 2014 P1: 3, 7, 9 […]
Leave a Comment

For 9i shouldn’t the vector be (-5 10 -10)
Sorry I’m careless