All solutions here are SUGGESTED. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions.
This is answers for H2 Mathematics (9740). H2 Mathematics (9758), click here.
Numerical Answers (click the questions for workings/explanation)
Question 1: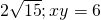 
Question 2: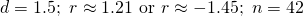 
Question 3: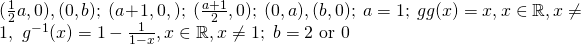 
Question 4: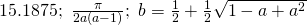 
Question 5: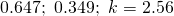 
Question 6: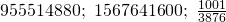 
Question 7: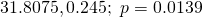 
; Do not reject 
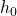, Not necessary.
Question 8: Model (D);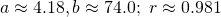 
Question 9: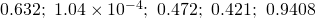 
Question 10: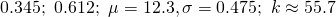 
(i)
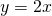
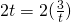
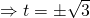
When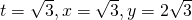 
When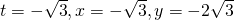 
Length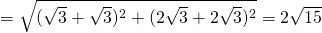 
units.
(ii)
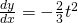
Tangent @ P: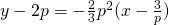 
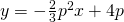
@D,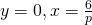 
@E,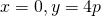 
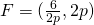
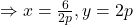
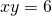
(i)
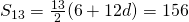
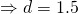
(ii)
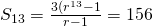
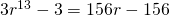
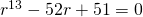
If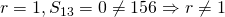 
Using GC,
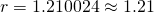
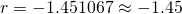
(iii)
![3(1.210024)^{n-1} > 100[3 + (n-1)(1.5)]](https://theculture.sg/wp-content/ql-cache/quicklatex.com-99369a82fe901d01dd092313a72b3e74_l3.png "Rendered by QuickLaTeX.com")
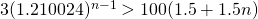
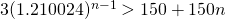
Using GC,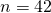 
(a)
(i)
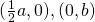
*For students: We half our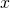 
values here as we scale by factor 
.
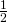x- intercept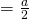 
y- intercept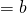 
(ii)
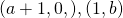
*For students: We plus one to our 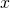values here as we translate by 1 unit in the positive x direction.
x- intercept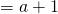 
y- intercept inconclusive
(iii)
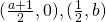
*For students: We plus one to our 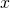values here as we translate by 1 unit in the positive x direction. Then, we half our 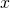values here as we scale by factor .
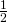x- intercept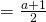 
y- intercept inconclusive
(iv)
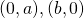
*For students: since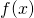 
and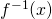 
is a reflection about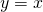 
x- intercept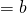
y- intercept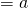 
(b)
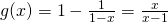
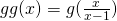
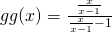
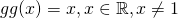
Let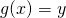 
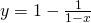
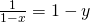
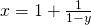
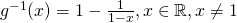
(iii)
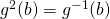
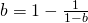
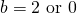
(a)
Area
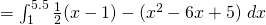
Using GC, Area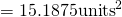 
(b)
(i)
Volume
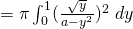
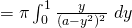
![= \frac{\pi}{2} \bigg[ \frac{1}{a-y^2} \bigg]_0^1](https://theculture.sg/wp-content/ql-cache/quicklatex.com-043f9725ae9338a1580454de201bc163_l3.png "Rendered by QuickLaTeX.com")
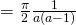
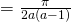
(ii)
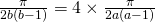
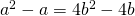
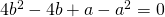
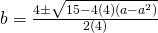
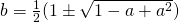
Since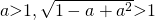 
, and volume has to be formed in a same way, 
,
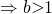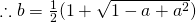
(i)
The average number of customers joining a supermarket checkout queue is a constant.
A customer joining a supermarket checkout is independent of another customer joining a supermarket checkout.
(ii)
Let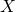 
denote the number of customers joining a supermarket checkout queue in a 5-minute period.
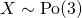
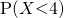
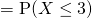
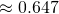
(iii)
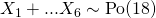
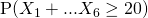
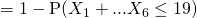
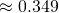
(iv)
Let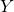 
denote the number of customers leaving a supermarket checkout queue in a 3-minute period.
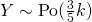
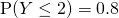
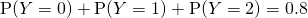
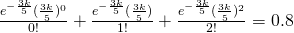
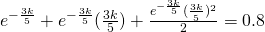
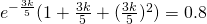
Using GC,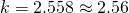 
(i)
Number of ways
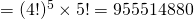
(ii)
Number of ways ![= [(3!)^3 \times 10! ]\times 2 = 1567641600](https://theculture.sg/wp-content/ql-cache/quicklatex.com-93a9d6e95b64bc27ab295b58b1bc1209_l3.png "Rendered by QuickLaTeX.com")
(iii)
Required probability
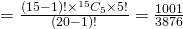
(i)
unbiased estimate of population mean
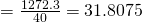
unbiased estimate of population variance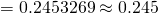 
(ii)
Let X denote the mass of biscuit bars, in grams
Let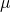 
denote the population mean mass of biscuit bars, in grams.
Test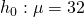 
against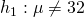 
at 1% level of significance
Under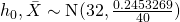 
approximately, by Central Limit Theorem.
Test Statistic,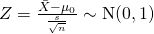 
Using GC,
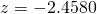
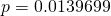
Since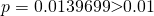 
, we do not reject 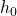at 1% level of significance and conclude with insufficient evidence that the mean mass differs from 32g.
(iv)
The sample size,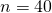 
is sufficiently large for the manager to approximate the the population distribution of the masses of the biscuit bars to a normal distribution by Central Limit Theorem.
(a)
(i)
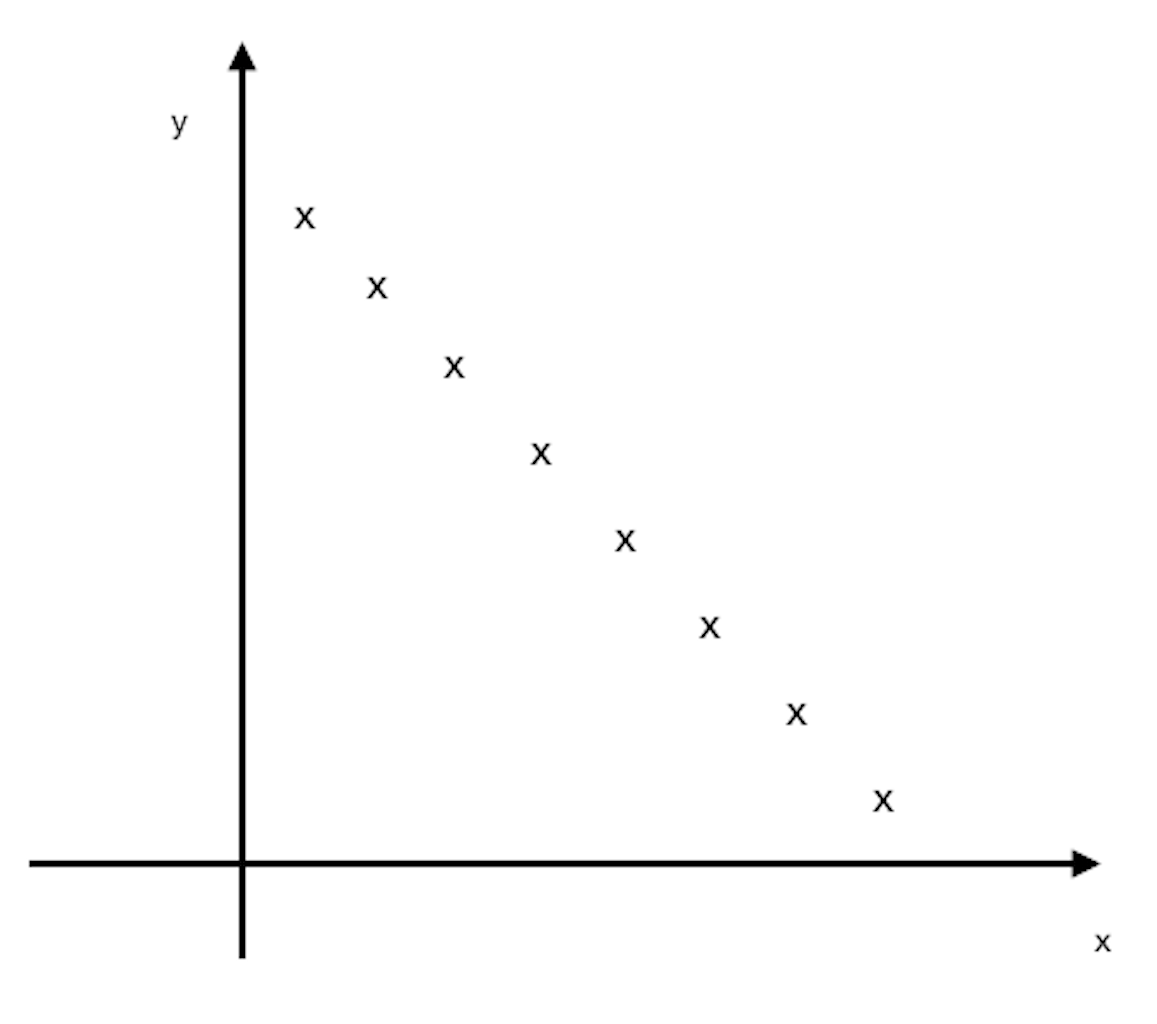
Graph of 8ai
(ii)
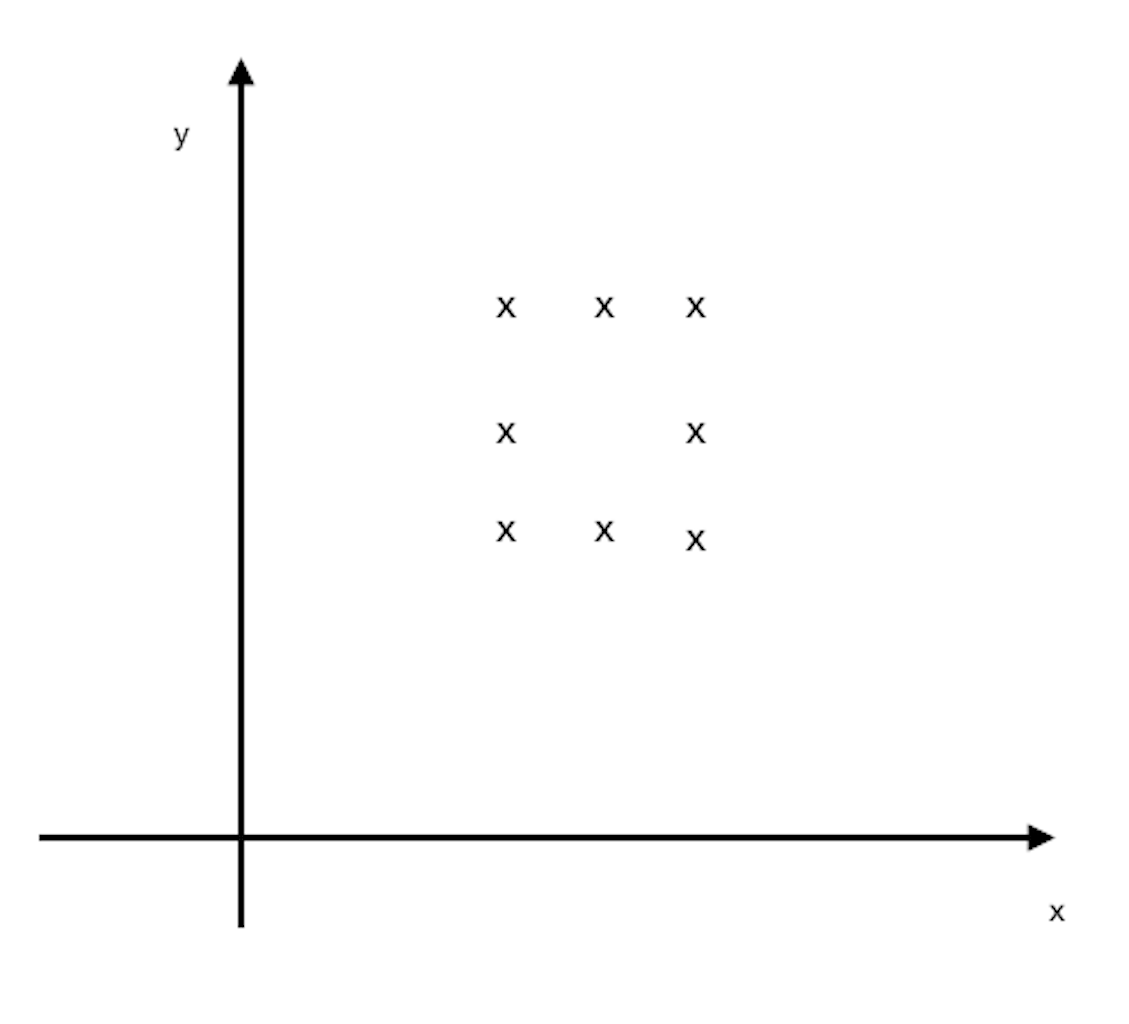
Graph of 8aii
(iii)
Graph of 8aiii
(b)
(i)
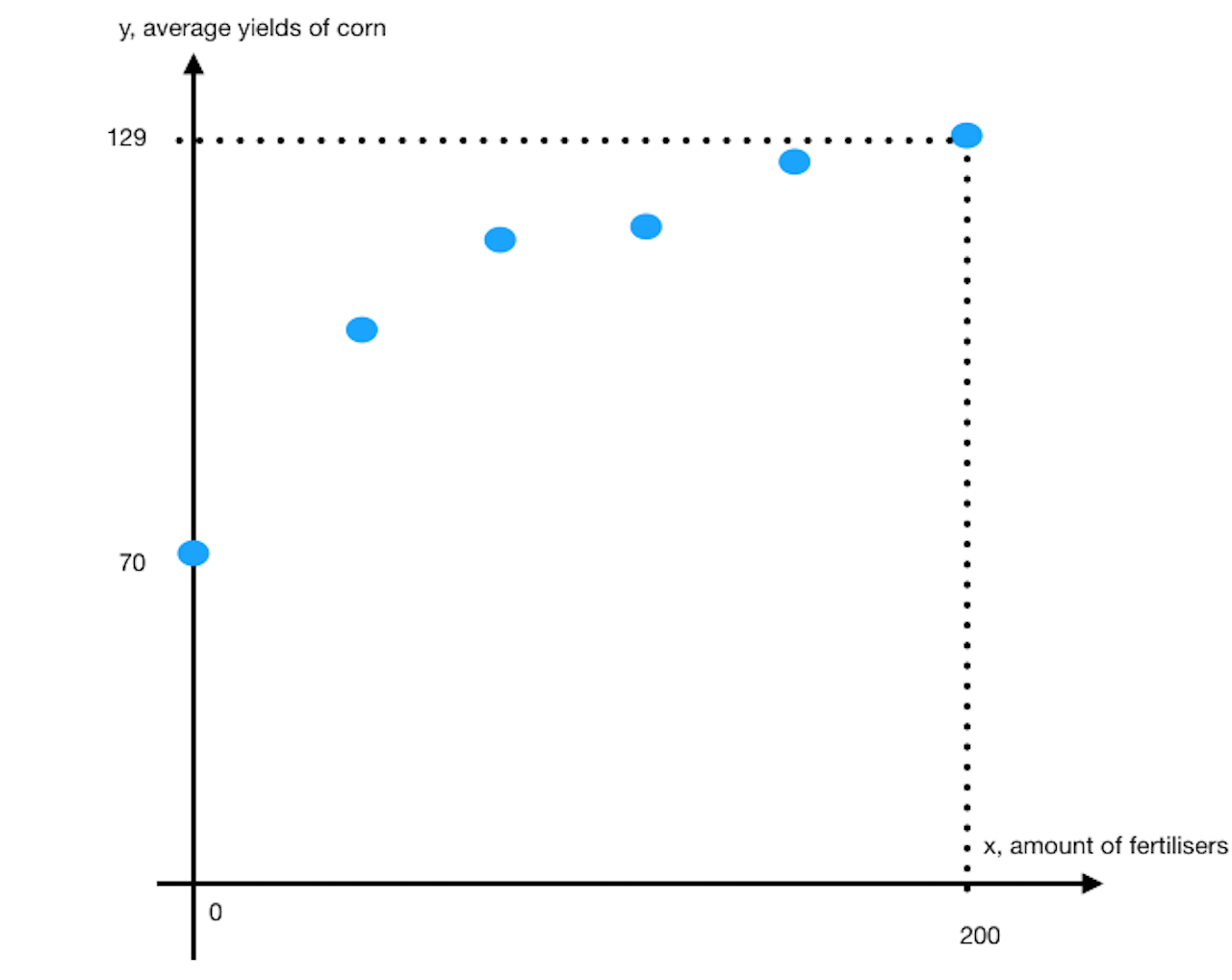
Graph of 8bi
Model (D) is appropriate.
(ii)
Using GC,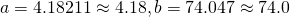 
and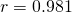 
(iii)
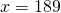is within given data range, and we are performing interpolation, which is a good practice.
The r value is close to 1 which suggest a strong positive linear correlation between the average yields of corn and the amount of fertiliser applied.
(i)
The probability that the lights are faulty is constant.
The event that the light is faulty is independent of another light being faulty.
The light can only be either faulty or non faulty.
(ii)
Let 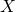denote the number of faulty lights in a box of 12.
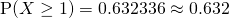
(iii)
Required probability ![= [\text{P}(X \ge 1) ]^20 = 1.0445 \times 10^{-4} \approx 1.04 \times 10^{-4}](https://theculture.sg/wp-content/ql-cache/quicklatex.com-baf0a11ee44be8ab043e2b3a524cbd29_l3.png "Rendered by QuickLaTeX.com")
(iv)
Let 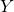denote the number of faulty lights in a carton of 240.
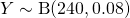
Since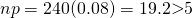 
and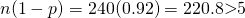 
,
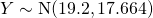approximately.
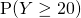
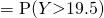by continuity correction
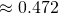
(v)
Events in (iii) is a subset of events in (iv).
(vi)
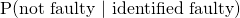
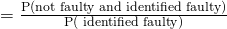
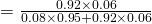
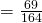
(vii)
Required Probability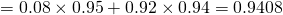 
(viii)
From (vii), the quick test seem to be 94% accurate. However, from (vi), we understand that out of the number of lights identified faulty, 42.1% of them will be a mistake. As such, the quick test is not worthwhile, since light identified as faulty are mistakingly discarded. Moreover it will cost money to administer a test.
(i)
Let
denote the mass of a sphere, in grams.
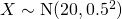
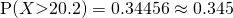
(ii)
Let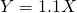 
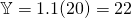
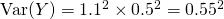
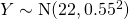
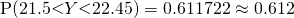
(iii)
Let 
denote the mass of a bar, in grams.
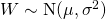
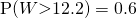
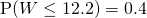
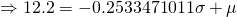— (1)
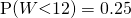
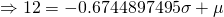— (2)
Using GC,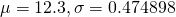 
Mean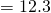 
g
Standard deviation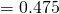 
g
(iv)
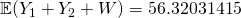
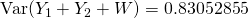
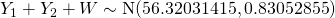
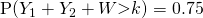
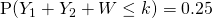
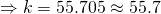g.
Relevant materials
MF26
KS Comments
Hi. Can you upload question 5 and 9iv/vii. These are the questions that differ from the other paper. Thankyou.
i dont have that paper. can send me at +65 9815 6827. I’ll do it.
Hello. I’ve sent you the papers. Please check 🙂
thank you
Hi! Do you still need the paper?
for 5 i got 0.647, 0.350 and some decimal for the k.
for 9iv i got 0.472 i think x>=19.5 by c.c
for 9vi is conditional prob and i said something about the margin of error being less than the probability of fault 0.08.
Hi, wondering for the hypothesis testing question, is the left tail test accepted? Because in the real world context, the most important thing is u<32? Because if they overstated their claim, they can get sued but if they understated it then it doesnt matter? Well thats my logic but i regretted overthinking and changing my answer during the exam
doubt it. It’s not about the company being sued, it’s about testing if the claim holds true. And since it’s two-tailed the critical region changes also.
Will there be ‘error carry forward’ marks?? For eg if part (iii) needs (ii) answers, but my answer for part (ii) was wrong??
Sorry is there any error for 9iii? When i key into GC i get approx 0.47154
yes, i made a mistake. sorry! Thank you 🙂
dont think the 9iv is correct? from gc value gives 0.472
yes, my bad. so sorry. typed wrongly. Thank you 🙂
Hi, is it okay for you to show the working for 4bi) using the substitution u= a-y^2? Thanks so much for your help! 🙂
Definitely. So Long as answer is correct 🙂
I’m so sorry. This may seem very pessimistic but I would just like to know, what do u think are the cutoffs for grades C and D? It would be really helpful.
Hello there. This might come off as very pessimistic, but do u by any chance have any idea what the marks range is going to be for grades C and D overall? Would be really helpful
i reckon is +8 to the normal grade boundaries. 🙂