I’ve covered some things in classes, with sufficient revisions and final lap papers set. So I thought we have a little breakdown. And of course, we should review what was weeded away in the 9740 H2 Mathematics Syllabus. After all, this is the very LAST time the can test them.
- Recurrence Relations. I’ve harped on this last year too. Conjectures! Conjectures! You can read more about it here. An a question involving conjecture should start with a recurrence relation, then a conjecture, ending with a recurrence MI. Students should know how to do both
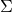and recurrence MI. Yes, they are different. Loci. You guys are the lucky last batch to do Loci. So please buy a protractor and compass. Draw them, as one of my student put it, surgically. If need be, use a graph paper (why not?). Harder loci for example can require students to draw for example,
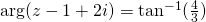. You should not have trouble measuring this angle, because you could not even be able to do it. Students should be able to draw such angles with ease. One little note about Loci, will definitely their geometrical descriptions. Many students can draw this, but stumble to describe them.Vectors. Truth be told, I’m still waiting for a question involving vectors in 3D, to land in A’levels. An example can be the HCI Prelims Paper 1 Question 6, which can be found here.
Poisson Distribution. I don’t know what this topic has been axed. So students should ready for one big Poisson Distribution questions, I say give it 12-14 marks. And it should be tested with conditional probability. I’ll practice either Demand & Supply or Inflow & Outflow questions. An example can be the one found in NYJC Prelims Paper 2 Question 11, which can be found here.
Correlation & Regression. Ever wondered what the
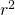means in the GC? Well, 
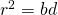is being removed from the syllabus as well. It hasn’t surfaced before, so maybe it shall finally make its one and only LAST presence felt this year. Students should familiarise themselves with the use of 
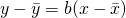equation, which can be found in the MF15. I know many of you probably have not seen it before.Hypothesis Testing. Students should review definitions of level of significance and p-value. Also understand what you may conclude from a Z-Test, using the results of a T-test. A little small part that students can think about, is why use a small sample size? After all, we know that have a sufficiently large
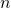allows us to perform CLT and then use a Z-Test.Trigonometry. After it appeared in 2011 for a trigonometry MI, the product to sum formulas is still a problem for most students. I highly doubt its coming out again with MI, but its can easily come out again with complex numbers. An example can be this.
More examples and discussion will be made in class.
[…] Thoughts before 2016 A-level H2 Mathematics […]
[…] Thoughts before 2016 A-level H2 Mathematics […]
Leave a Comment
hi when are we supposed to use CLT? how about when pop var is unknown but n large? and do we explicitly have to state it in the working or only when the question asks in a separate part? also the assumptions that n is normally distributed, do we need to explicitly state?
Hi, I assume you’re referring to Hypothesis Testing here. You should explicitly state the use of CLT in the working for your Hypothesis testing, for the flow of working. Assumption that X (not n) is normally distributed should be stated in the workings too, when necessary. Just note that you cannot assume it is normally distributed and do CLT at the same time.
When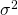
is unknown and n is large, we can do CLT to approximate X to normal distribution.
Lastly, to do CLT, we need to satisfy BOTH conditions that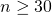
and X follows a non-normal distribution. Distributions that are non-normal are Binomial and Poisson, typically if we need to find the Sample Mean/ Average of a binomial or Poisson Distribution, we should consider CLT.