Why we need to be close to zero?

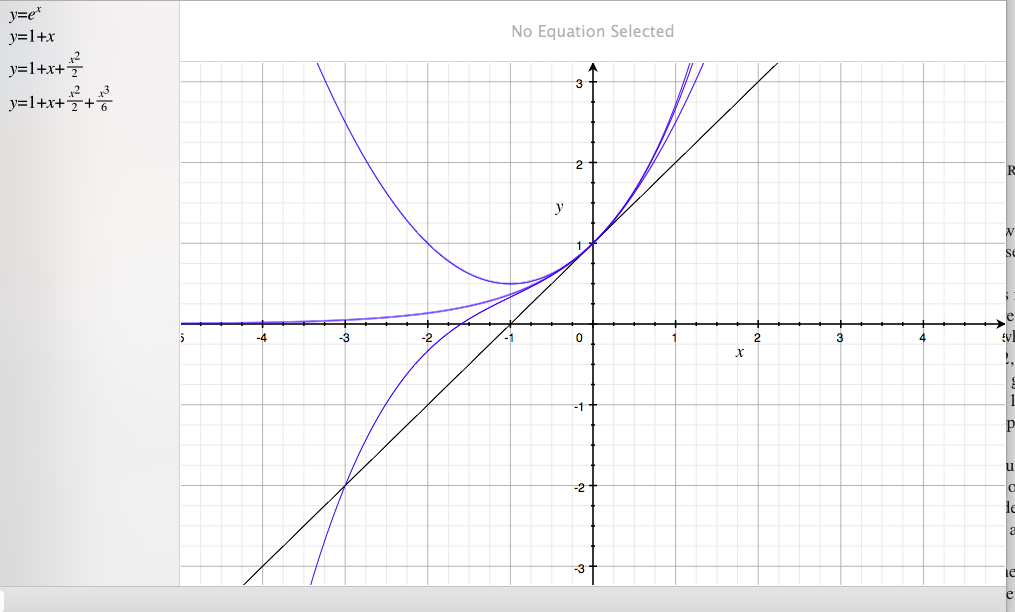
Many students have asked me why it is important to for $x$ to be close to zero for the Maclaurin’s expansion to be a good approximation. So here, I plot it in the 4 curves:
$y =e^x$ which is our actual curve.
$y = 1+x$ which is the estimation of $e^x$ , up to and including $x$ .
$y = 1+x+\frac{x^2}{w!}$ which is the estimation of $e^x$ , up to and including $x^2$ .
$y = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}$ which is the estimation of $e^x$ , up to and including $x^3$ .

Curves and its estimation

We can observe from the graphs, that as we increase the degree of order, the estimated curves become more like that of $e^x$ , although it still tend to deviate a lot. The idea of maclaurin’s is that it provides us a way to interpolate and write the humble $e^x$ equation out in a polynomial that actually never ends. So as we continue to consider more terms, our estimation will get close and closer to the actual curve.

And clearly, we see that when $x=0$ , we found the actual value. This is simply because the maclaurin’s expansion is centred about zero. 🙂

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Comments

pingbacks / trackbacks

List of Great and Helpful Math Articles – The Culture SG
[…] Why we need to be close to zero for an approximation to be good? […]
March 9th, 2017 01:23 PM

Cart

Why we need to be close to zero?

Leave a Comment
Cancel reply

Why we need to be close to zero?

Leave a Comment Cancel reply

Leave a Comment
Cancel reply