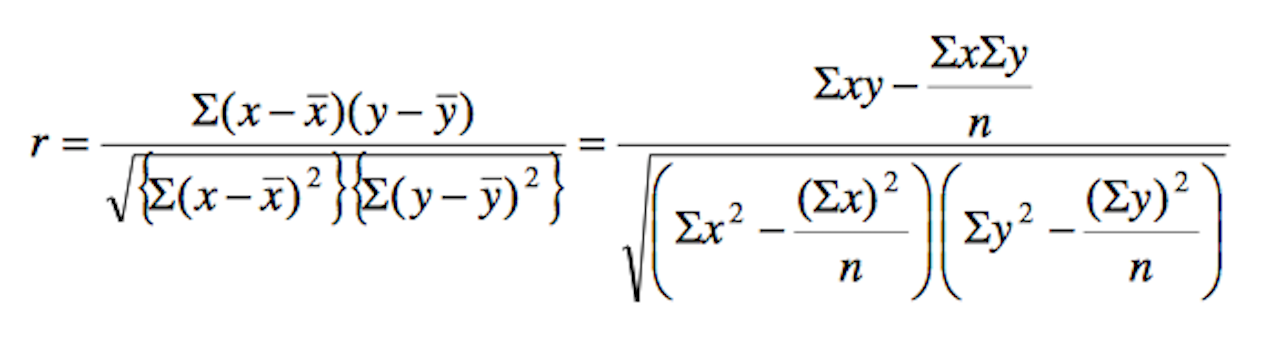If you missed part 1, you should read that first. Lets look at why r-value is independent of translation and scaling from the mathematical approach.
Credits: MF15
Consider 
so 
is a scaling parameter while 
is a translation parameter. Notice first we can re-write the formula like this.
![\frac {\sum(x-\sum(\frac{x}{n}))(y-\bar{y})}{\sqrt{[\sum(x-\sum{\frac{x}{n}})^2][\sum(y-\bar{y})^2]}}&s=3](http://theculture.sg/wp-content/ql-cache/quicklatex.com-42b8d1404e04929df475cbe8ace93b14_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum({aw+b}-\sum(\frac{aw+b}{n}))(y-\bar{y})}{\sqrt{[\sum({aw+b}-\sum{\frac{aw+b}{n}})^2][\sum(y-\bar{y})^2]}}&s=3](http://theculture.sg/wp-content/ql-cache/quicklatex.com-a27cf1533deea3ab2e18a7a6f5bc88de_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum({aw+b}-\sum(\frac{aw}{n})-b)(y-\bar{y})}{\sqrt{[\sum({aw+b}-\sum{\frac{aw}{n}}-b)^2][\sum(y-\bar{y})^2]}}&s=3](http://theculture.sg/wp-content/ql-cache/quicklatex.com-3998caf21d219f50dafc3ec262d0306b_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum({aw}-\sum(\frac{aw}{n}))(y-\bar{y})}{\sqrt{[\sum({aw}-\sum{\frac{aw}{n}})^2][\sum(y-\bar{y})^2]}}&s=3](http://theculture.sg/wp-content/ql-cache/quicklatex.com-f1ee039313960ce71d049083fe196278_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum({aw}-a\sum(\frac{w}{n}))(y-\bar{y})}{\sqrt{[\sum({aw}-a\sum{\frac{w}{n}})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-96f4d34cf62410412660d8120271fff4_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum({aw}-a\bar{w})(y-\bar{y})}{\sqrt{[\sum({aw}-a\bar{w})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-8388114e030e1b2b36978c2454fa8df4_l3.png "Rendered by QuickLaTeX.com")
![=\frac {a\sum(w-\bar{w})(y-\bar{y})}{\sqrt{[a^{2}\sum(w-\bar{w})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-79518c7c64be2deb5ec3ded1da097961_l3.png "Rendered by QuickLaTeX.com")
![=\frac {a\sum(w-\bar{w})(y-\bar{y})}{\sqrt{a^2} \sqrt{\sum(w-\bar{w})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-d3d8ae12c5208d0d343c41cd117b4d89_l3.png "Rendered by QuickLaTeX.com")
![=\frac {a\sum(w-\bar{w})(y-\bar{y})}{a\sqrt{\sum(w-\bar{w})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-9f0a82082115b2d7e7c10ef07ce487ba_l3.png "Rendered by QuickLaTeX.com")
![=\frac {\sum(w-\bar{w})(y-\bar{y})}{\sqrt{\sum(w-\bar{w})^2][\sum(y-\bar{y})^2]}}](http://theculture.sg/wp-content/ql-cache/quicklatex.com-2482fbaec09cd78e4ad79ae15cc50474_l3.png "Rendered by QuickLaTeX.com")
We finally end up with the conclusion that the r-value will have no change at all! I hope this explains why r-value is independent of scaling and translation. Do leave comments should you have other methods!
