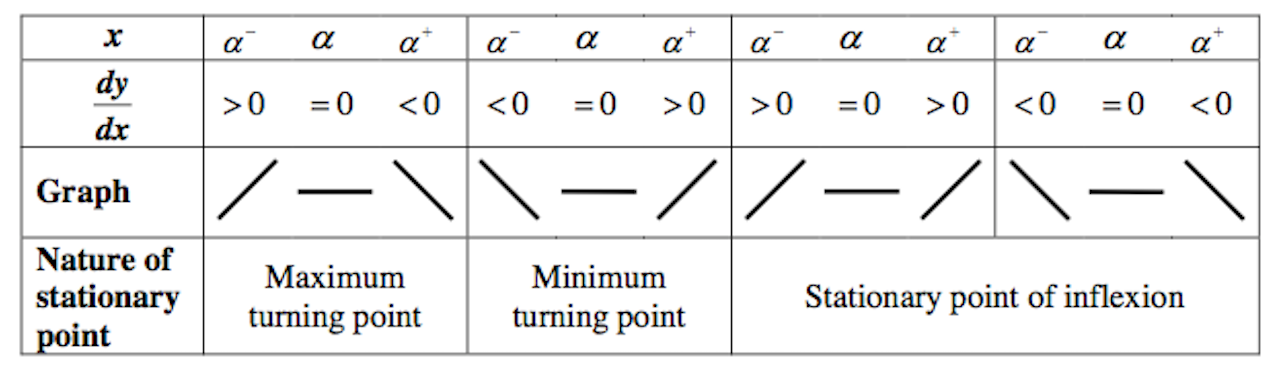
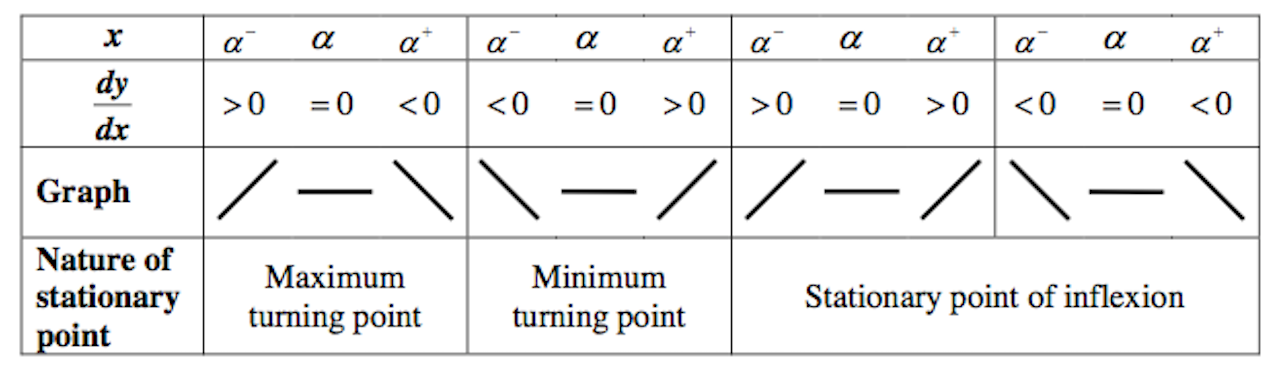
When 
, it implies we have a stationary point.
To determine the nature of the stationary point, we can do either the first derivative test or the second derivative.
The first derivative test:
First Derivative Test
Students should write the actual values of 
and 
in the table.
We use this under these two situations:
1. 
is difficult to solve for, that is, is tough to be differentiated
2. 
The second derivative test:
Second Derivative Test
Other things students should take note is concavity and drawing of the derivative graph.
