All solutions here are suggested. Mr. Teng will hold no liability for any errors. Comments are entirely personal opinions
Numerical Answers (workings/explanations are after the numerical answers.)
Question 1:
Question 2:
Question 3:
Question 4:
Question 5:
Question 6:
Question 7: ![]() c decreases by
c decreases by ![]()
Question 8: ![]()
Question 9: ![]()
Question 10: ![]()
Question 11: ![]()
Question 12: ![]()
Question 13: ![]()
(a)
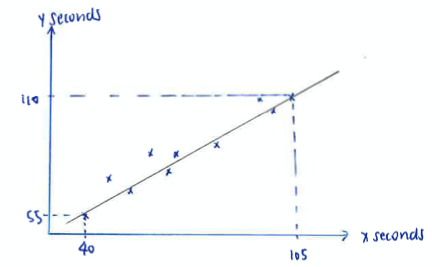
(b)
Using GC, product moment correlation coefficient ![]() (3 dp)
(3 dp)
(c)
Using GC, ![]()
![]() (2 sf)
(2 sf)
(d)
Let ![]() seconds
seconds
The estimate is reliable since ![]() is within the given data range and interpolation produces a reliable estimate.
is within the given data range and interpolation produces a reliable estimate.
(e)![]() will be unchanged since there are no change in scale of measurement.
will be unchanged since there are no change in scale of measurement.![]() will be reduced by
will be reduced by ![]() units.
units.
Note: ![]() is unchanged (since it is independent of scale of measurement)
is unchanged (since it is independent of scale of measurement)
(a)
Number of ways ![]() ways
ways
(b)
Number of ways ![]() ways
ways
(a)
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(b)![]()
![]()
![]()
![]()
(a)
Let masses of red, green and yellow peppers be ![]() respectively.
respectively.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(b)![]()
![]()
![]()
![]()
![]()
(c)
Required probability![]()
![]()
![]()
(d)![]()
Let ![]() be the number of green peppers with mass more than 220g, out of 20.
be the number of green peppers with mass more than 220g, out of 20.![]()
![]()
(a)(i)
Since ![]() , then
, then ![]() . Thus, both events
. Thus, both events ![]() and
and ![]() cannot be mutually exclusive.
cannot be mutually exclusive.
(a)(ii)
Since ![]() and
and ![]() are independent,
are independent, ![]()
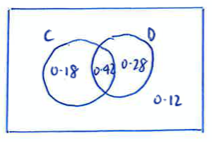
(b)(i)![]()
![]()
![]()
![]()
![]()
![]()
(b)(ii)![]()
![]()
(b)(iii)![]()
![]()
![]()
![]()
![]()
(a)
unbiased estimate of population mean,
unbiased estimate of population variance,
Let
Test
Under
Test Statistic,
Reject
Using GC,
Since
(b)
Let standard deviation of sample be
Under
For
Since
Since
(a)
unbiased estimate of population mean ![]()
unbiased estimate of population variance ![]()
(b)
Since ![]() is large, by central limit theorem,
is large, by central limit theorem, ![]() approximately
approximately
Required probability ![]()
Assume that the unbiased estimates of the population mean and variance calculated in (a) are good estimates for the eggs in (b)
Assume that the masses of the eggs in the randomly chosen tray are independently and identically distributed.
(c)
Let ![]() be the number of trays with mean mass of an egg lying between 61g and 63g, out of 10.
be the number of trays with mean mass of an egg lying between 61g and 63g, out of 10.![]()
Required probability ![]()
