Random Questions from 2016 Prelims #4

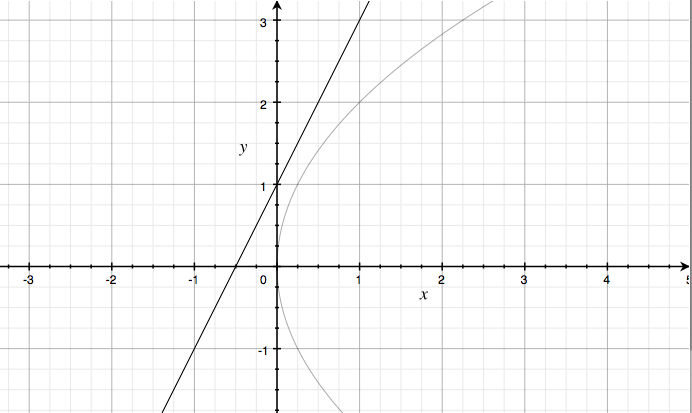
VJC P1 Q6

A curve has equation $y^2=4x$ and a line $l$ has equation $2x-y+1=0$ as shown above.

$B(b, 2\sqrt{b})$ is a fixed point on C and A is an arbitrary point on $l$ . State the geometrical relationship between the line segment AB and $l$ is the distance from B to A is the least.

Taking the coordinates of A as $(a, 2a+1)$ , find an equation relating $a$ and $b$ for which AB is the least.

Deduce that when AB is the least, $(AB)^2 = m (2b - 2\sqrt{b} +1)^2$ where $m$ is a constant to be found. Hence or otherwise, find the coordinates of the point on C that is nearest on $l$ .

Solution

About

KS Teng

KS has been teaching H2/H1 Mathematics and IB mathematics for the more than 10 years. Having taught students from all various Junior Colleges, KS adapts to students' abilities and help them better understand the topics. As someone who loves to teach mathematics and sees it as a truly useful tool in life, KS seeks to enable students to appreciate math. Therefore, his tuition mission is to motivate and cultivate students to be independent and confident thinkers.

Random Questions from 2016 Prelims #4

Leave a Comment Cancel reply

Leave a Comment
Cancel reply