This page contains all questions and answers asked by students from this class. The most recent questions will be at the top.
Vectors Q7 [Homework]
(i)
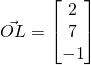
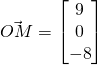
Using ratio theorem, 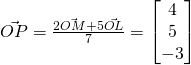
Since ![]() is perpendicular to
is perpendicular to ![]()
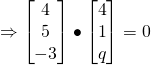
![]()
(ii)
To be a parallelogram, ![]()
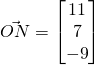
![]()
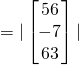
![]()
(iii)
Let 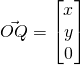
Since ![]()
![]() — (1)
— (1)
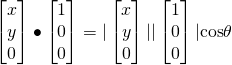 — (2)
— (2)
Solving, ![]()
![]()
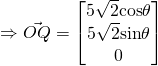
Vectors Q8 [Homework]
(i)
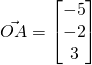
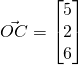
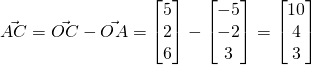
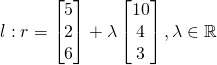
(ii)
Let R be the top of the vertical pillar,
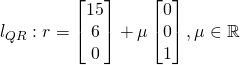
Since R is collinear with A and C, R is the intersection of line AC and QR.
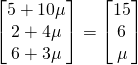
![]()
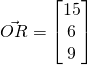 , and the height is 9m.
, and the height is 9m.
(iii)
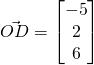
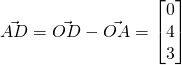
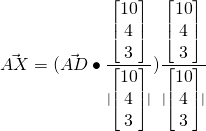
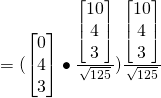
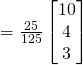
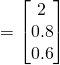
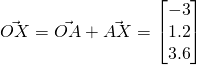
Vectors Q9 [Homework]
(i)
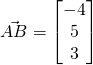
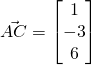
Normal of 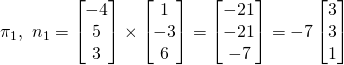
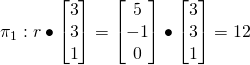
(ii)
Let ![]() be the acute angle
be the acute angle
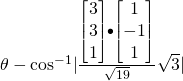
![]()
(iii)
![]() — (1)
— (1)
![]() — (2)
— (2)
Using GC, 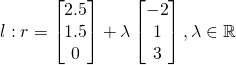
(iv)
Let ![]() be the normal of
be the normal of ![]()
Length of projection ![]()
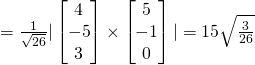
(v)
Required distance ![]()
(vi)
Let normal of 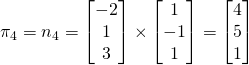
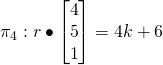
If ![]() intersect at l,n
intersect at l,n![]() lies on
lies on ![]()
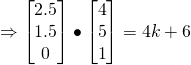
![]()
